Convergence Tests
Convergence tests are implemented in /validation/convergence_tests and range from zero-dimensional time-stepper tests to two-dimensional integration tests that involve non-trivial pressure fields, advection, and diffusion.
For all tests except point exponential decay, we use the
and
to compare simulated fields,
Point Exponential Decay
This test analyzes time-stepper convergence by simulating the zero-dimensional, or spatially-uniform equation
with the initial condition
We find the expected first-order convergence with decreasing time-step
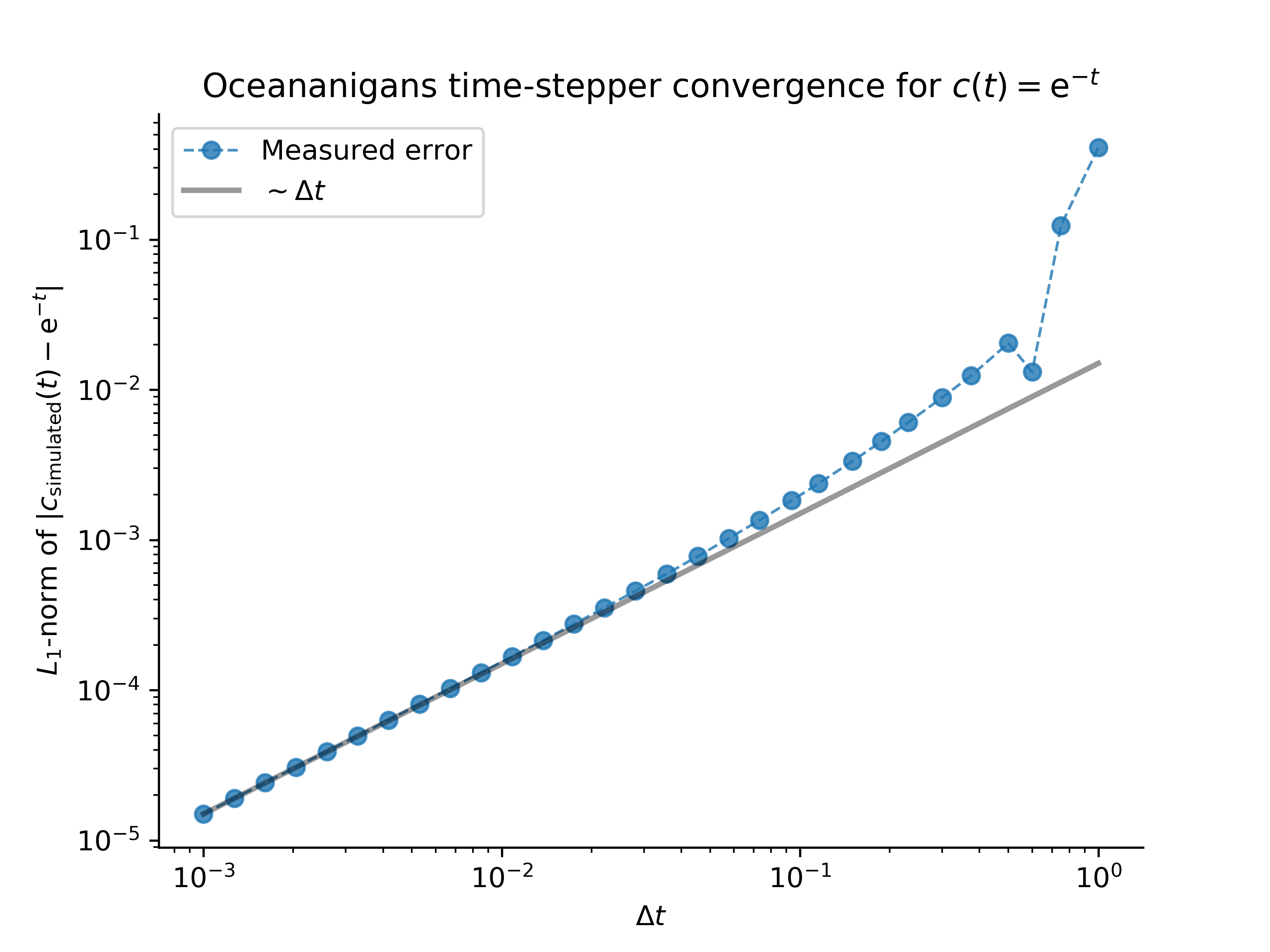
This result validates the correctness of the Oceananigans implementation of Adams-Bashforth time-stepping.
One-dimensional advection and diffusion of a Gaussian
This and the following tests focus on convergence with grid spacing,
In one dimension with constant diffusivity
For this test we take the initial time as
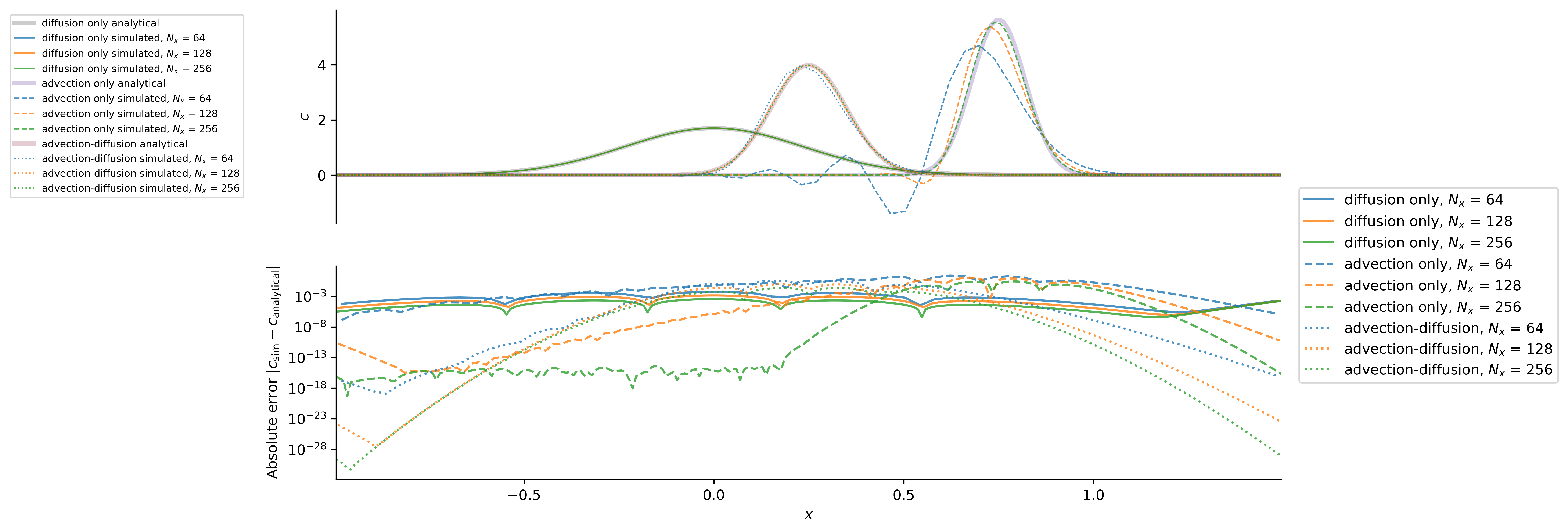
which exhibit the expected second-order convergence with
These results validate the correctness of time-stepping, constant diffusivity operators, and advection operators.
One-dimensional advection and diffusion of a cosine
In one dimension with constant diffusivity
The solutions are
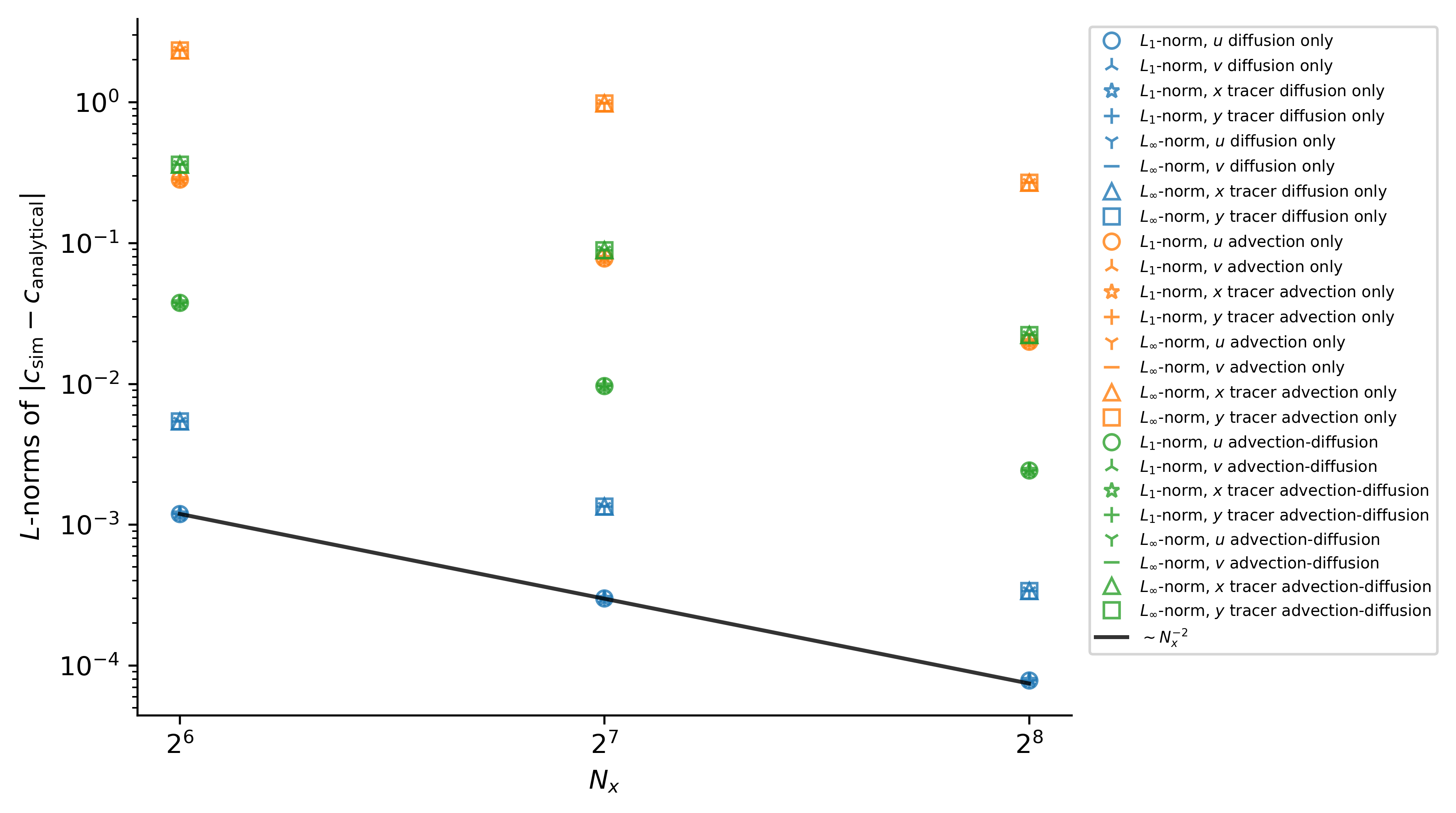
which exhibit the expected second-order convergence with
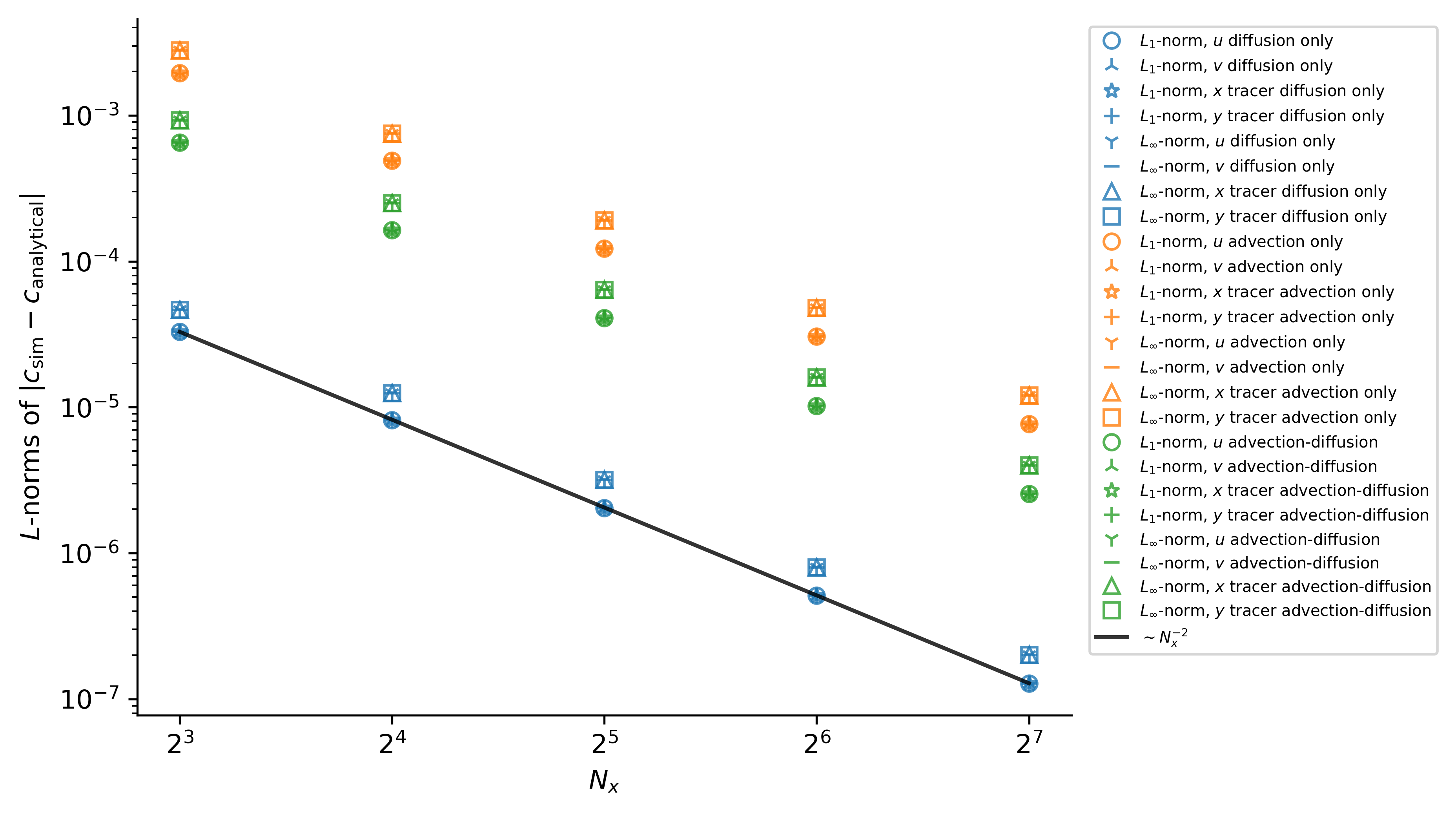
These results validate the correctness of time-stepping, constant diffusivity operators, and advection operators.
Two-dimensional diffusion
With zero velocity field and constant diffusivity
decays according to
with either periodic boundary conditions, or insulating boundary conditions in either
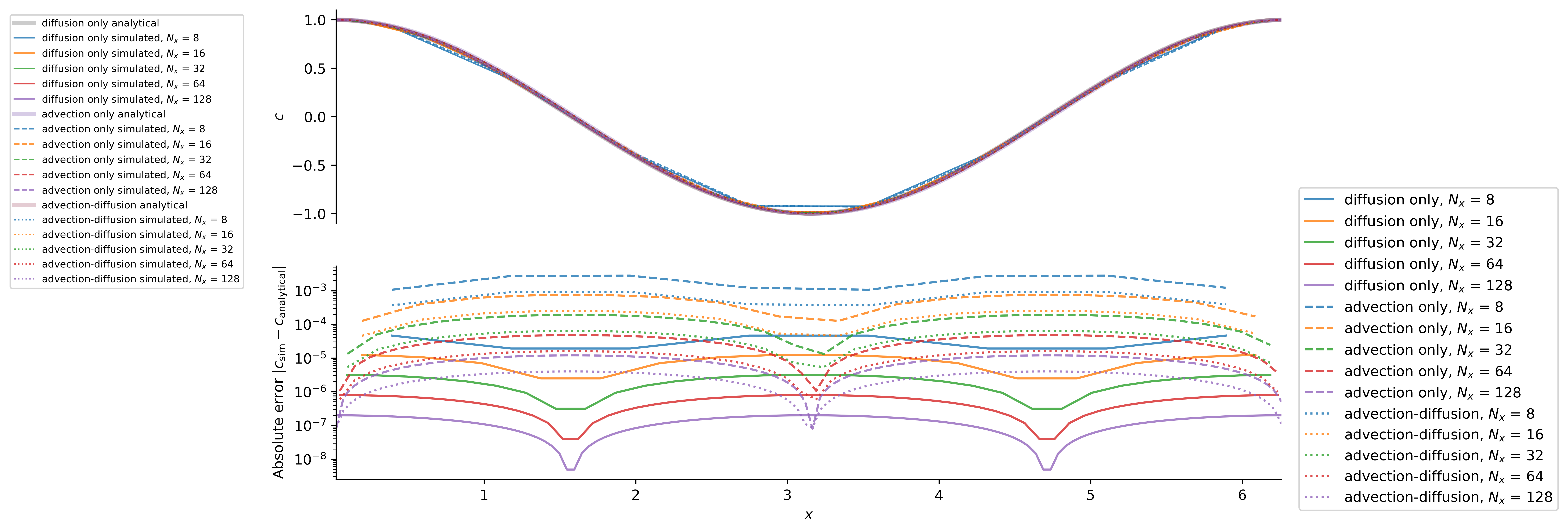
The expected convergence with
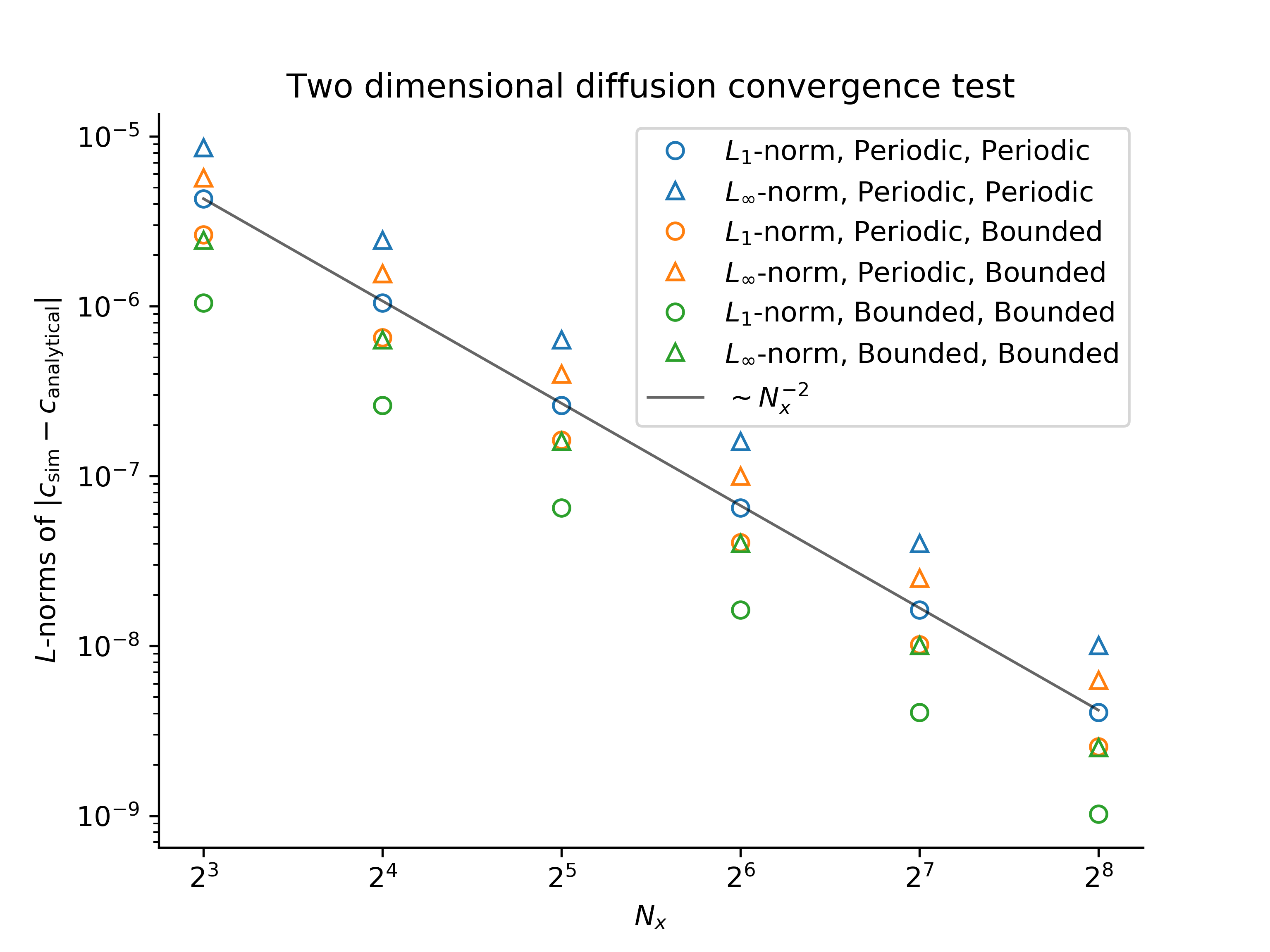
This validates the correctness of multi-dimensional diffusion operators.
Decaying, advected Taylor-Green vortex
The velocity field
is a solution to the Navier-Stokes equations with viscosity
The expected convergence with spatial resolution is observed:
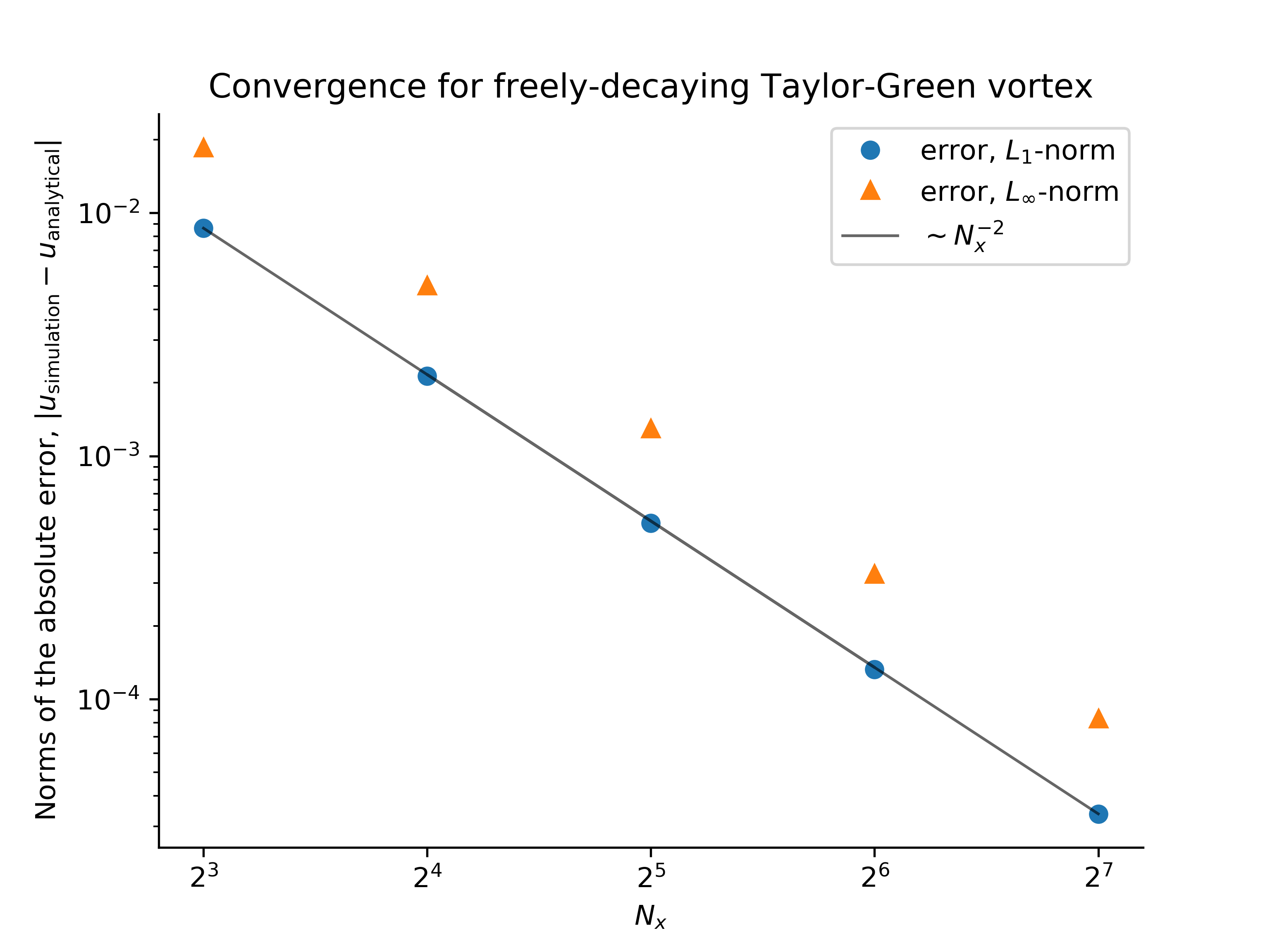
This validates the correctness of the advection and diffusion of a velocity field.
Forced two-dimensional flows
We introduce two convergence tests associated with forced flows in domains that are bounded in
Note: in this section, subscripts are used to denote derivatives to make reading and typing equations easier.
In a two-dimensional flow in
where subscript denote derivatives such that
while the equation for vorticity,
Finally, taking the divergence of the momentum equation, we find a Poisson equation for pressure,
To pose the problem, we first pick a streamfunction
We restrict ourselves to a class of problems in which
Grinding through the algebra, this particular form implies that
where primes denote derivatives of functions of a single argument. Setting
then the pressure Poisson equation becomes
This completes the specification of the problem.
We set up the problem by imposing the time-dependent forcing functions
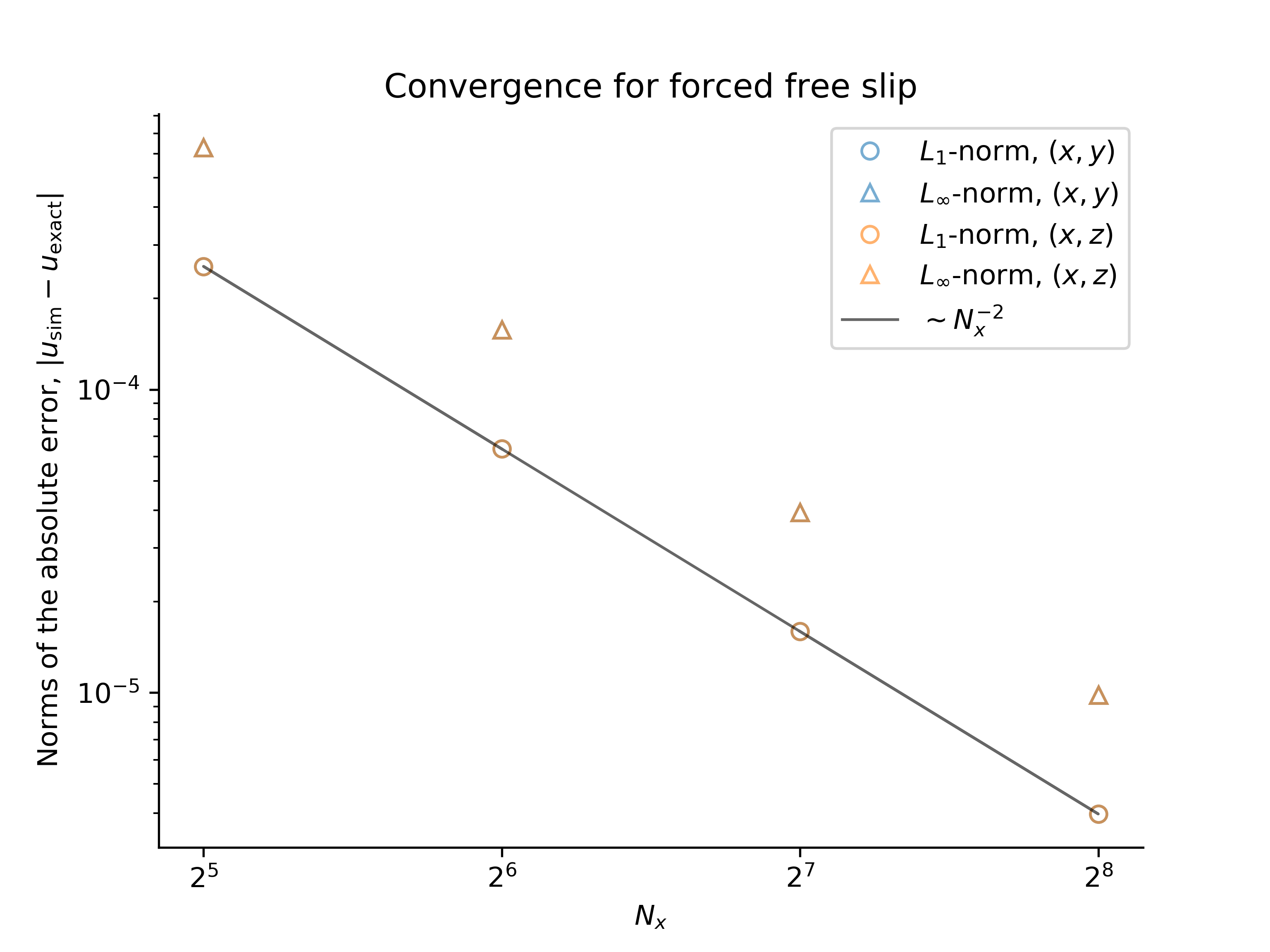
The convergence tests are performed using both
Forced, free-slip flow
A forced flow satisfying free-slip conditions at
and thus
which satisfies the boundary conditions
which implies that
and
Forced, fixed-slip flow
A forced flow satisfying "fixed-slip" boundary conditions at
and thus
which satisfies the boundary conditions
The vorticity forcing is
which implies that
and
We set up the problem in the same manner as the forced, free-slip problem above. Note that we also must the no-slip boundary condition
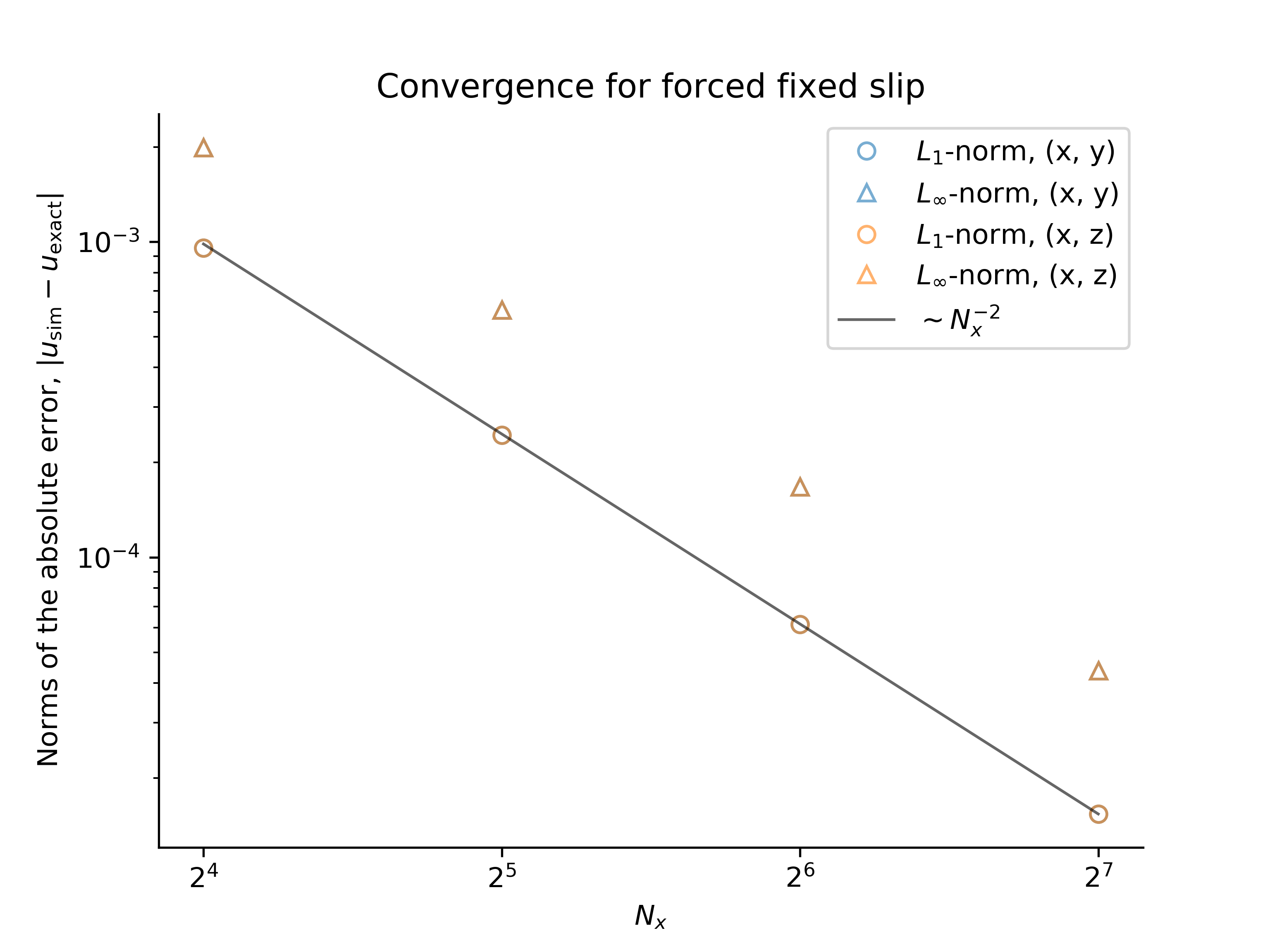
The convergence tests are performed using both