Baroclinic adjustment

In this example, we simulate the evolution and equilibration of a baroclinically unstable front.

Install dependencies

First let's make sure we have all required packages installed.

using Pkg
pkg"add Oceananigans, CairoMakie"

using Oceananigans
using Oceananigans.Units

Grid

We use a three-dimensional channel that is periodic in the x direction:

Lx = 1000kilometers # east-west extent [m]
Ly = 1000kilometers # north-south extent [m]
Lz = 1kilometers    # depth [m]

grid = RectilinearGrid(size = (48, 48, 8),
                       x = (0, Lx),
                       y = (-Ly/2, Ly/2),
                       z = (-Lz, 0),
                       topology = (Periodic, Bounded, Bounded))

48×48×8 RectilinearGrid{Float64, Periodic, Bounded, Bounded} on CPU with 3×3×3 halo
├── Periodic x ∈ [0.0, 1.0e6)          regularly spaced with Δx=20833.3
├── Bounded  y ∈ [-500000.0, 500000.0] regularly spaced with Δy=20833.3
└── Bounded  z ∈ [-1000.0, 0.0]        regularly spaced with Δz=125.0

Model

We built a HydrostaticFreeSurfaceModel with an ImplicitFreeSurface solver. Regarding Coriolis, we use a beta-plane centered at 45° South.

model = HydrostaticFreeSurfaceModel(; grid,
                                    coriolis = BetaPlane(latitude = -45),
                                    buoyancy = BuoyancyTracer(),
                                    tracers = :b,
                                    momentum_advection = WENO(),
                                    tracer_advection = WENO())

HydrostaticFreeSurfaceModel{CPU, RectilinearGrid}(time = 0 seconds, iteration = 0)
├── grid: 48×48×8 RectilinearGrid{Float64, Periodic, Bounded, Bounded} on CPU with 3×3×3 halo
├── timestepper: QuasiAdamsBashforth2TimeStepper
├── tracers: b
├── closure: Nothing
├── buoyancy: BuoyancyTracer with ĝ = NegativeZDirection()
├── free surface: ImplicitFreeSurface with gravitational acceleration 9.80665 m s⁻²
│   └── solver: FFTImplicitFreeSurfaceSolver
├── advection scheme: 
│   ├── momentum: WENO{3, Float64, Float32}(order=5)
│   └── b: WENO{3, Float64, Float32}(order=5)
└── coriolis: BetaPlane{Float64}

We start our simulation from rest with a baroclinically unstable buoyancy distribution. We use ramp(y, Δy), defined below, to specify a front with width Δy and horizontal buoyancy gradient M². We impose the front on top of a vertical buoyancy gradient N² and a bit of noise.

"""
    ramp(y, Δy)

Linear ramp from 0 to 1 between -Δy/2 and +Δy/2.

For example:
```
            y < -Δy/2 => ramp = 0
    -Δy/2 < y < -Δy/2 => ramp = y / Δy
            y >  Δy/2 => ramp = 1
```
"""
ramp(y, Δy) = min(max(0, y/Δy + 1/2), 1)

N² = 1e-5 # [s⁻²] buoyancy frequency / stratification
M² = 1e-7 # [s⁻²] horizontal buoyancy gradient

Δy = 100kilometers # width of the region of the front
Δb = Δy * M²       # buoyancy jump associated with the front
ϵb = 1e-2 * Δb     # noise amplitude

bᵢ(x, y, z) = N² * z + Δb * ramp(y, Δy) + ϵb * randn()

set!(model, b=bᵢ)

Let's visualize the initial buoyancy distribution.

using CairoMakie
set_theme!(Theme(fontsize = 20))

# Build coordinates with units of kilometers
x, y, z = 1e-3 .* nodes(grid, (Center(), Center(), Center()))

b = model.tracers.b

fig, ax, hm = heatmap(view(b, 1, :, :),
                      colormap = :deep,
                      axis = (xlabel = "y [km]",
                              ylabel = "z [km]",
                              title = "b(x=0, y, z, t=0)",
                              titlesize = 24))

Colorbar(fig[1, 2], hm, label = "[m s⁻²]")

fig

Simulation

Now let's build a Simulation.

simulation = Simulation(model, Δt=20minutes, stop_time=20days)

Simulation of HydrostaticFreeSurfaceModel{CPU, RectilinearGrid}(time = 0 seconds, iteration = 0)
├── Next time step: 20 minutes
├── Elapsed wall time: 0 seconds
├── Wall time per iteration: NaN days
├── Stop time: 20 days
├── Stop iteration: Inf
├── Wall time limit: Inf
├── Minimum relative step: 0.0
├── Callbacks: OrderedDict with 4 entries:
│   ├── stop_time_exceeded => 4
│   ├── stop_iteration_exceeded => -
│   ├── wall_time_limit_exceeded => e
│   └── nan_checker => }
├── Output writers: OrderedDict with no entries
└── Diagnostics: OrderedDict with no entries

We add a TimeStepWizard callback to adapt the simulation's time-step,

conjure_time_step_wizard!(simulation, IterationInterval(20), cfl=0.2, max_Δt=20minutes)

Also, we add a callback to print a message about how the simulation is going,

using Printf

wall_clock = Ref(time_ns())

function print_progress(sim)
    u, v, w = model.velocities
    progress = 100 * (time(sim) / sim.stop_time)
    elapsed = (time_ns() - wall_clock[]) / 1e9

    @printf("[%05.2f%%] i: %d, t: %s, wall time: %s, max(u): (%6.3e, %6.3e, %6.3e) m/s, next Δt: %s\n",
            progress, iteration(sim), prettytime(sim), prettytime(elapsed),
            maximum(abs, u), maximum(abs, v), maximum(abs, w), prettytime(sim.Δt))

    wall_clock[] = time_ns()

    return nothing
end

add_callback!(simulation, print_progress, IterationInterval(100))

Diagnostics/Output

Here, we save the buoyancy, $b$, at the edges of our domain as well as the zonal ($x$) average of buoyancy.

u, v, w = model.velocities
ζ = ∂x(v) - ∂y(u)
B = Average(b, dims=1)
U = Average(u, dims=1)
V = Average(v, dims=1)

filename = "baroclinic_adjustment"
save_fields_interval = 0.5day

slicers = (east = (grid.Nx, :, :),
           north = (:, grid.Ny, :),
           bottom = (:, :, 1),
           top = (:, :, grid.Nz))

for side in keys(slicers)
    indices = slicers[side]

    simulation.output_writers[side] = JLD2Writer(model, (; b, ζ);
                                                 filename = filename * "_$(side)_slice",
                                                 schedule = TimeInterval(save_fields_interval),
                                                 overwrite_existing = true,
                                                 indices)
end

simulation.output_writers[:zonal] = JLD2Writer(model, (; b=B, u=U, v=V);
                                               filename = filename * "_zonal_average",
                                               schedule = TimeInterval(save_fields_interval),
                                               overwrite_existing = true)

JLD2Writer scheduled on TimeInterval(12 hours):
├── filepath: baroclinic_adjustment_zonal_average.jld2
├── 3 outputs: (b, u, v)
├── array_type: Array{Float32}
├── including: [:grid, :coriolis, :buoyancy, :closure]
├── file_splitting: NoFileSplitting
└── file size: 32.5 KiB

Now we're ready to run.

@info "Running the simulation..."

run!(simulation)

@info "Simulation completed in " * prettytime(simulation.run_wall_time)

[ Info: Running the simulation...
[ Info: Initializing simulation...
[00.00%] i: 0, t: 0 seconds, wall time: 51.096 seconds, max(u): (0.000e+00, 0.000e+00, 0.000e+00) m/s, next Δt: 20 minutes
[ Info:     ... simulation initialization complete (47.174 seconds)
[ Info: Executing initial time step...
[ Info:     ... initial time step complete (21.660 seconds).
[06.94%] i: 100, t: 1.389 days, wall time: 47.117 seconds, max(u): (1.277e-01, 1.115e-01, 1.497e-03) m/s, next Δt: 20 minutes
[13.89%] i: 200, t: 2.778 days, wall time: 852.694 ms, max(u): (2.167e-01, 1.715e-01, 1.719e-03) m/s, next Δt: 20 minutes
[20.83%] i: 300, t: 4.167 days, wall time: 767.926 ms, max(u): (2.887e-01, 2.496e-01, 1.757e-03) m/s, next Δt: 20 minutes
[27.78%] i: 400, t: 5.556 days, wall time: 772.375 ms, max(u): (3.685e-01, 3.277e-01, 1.785e-03) m/s, next Δt: 20 minutes
[34.72%] i: 500, t: 6.944 days, wall time: 736.436 ms, max(u): (4.224e-01, 4.401e-01, 1.911e-03) m/s, next Δt: 20 minutes
[41.67%] i: 600, t: 8.333 days, wall time: 764.238 ms, max(u): (5.292e-01, 6.259e-01, 2.228e-03) m/s, next Δt: 20 minutes
[48.61%] i: 700, t: 9.722 days, wall time: 804.381 ms, max(u): (7.205e-01, 9.930e-01, 2.933e-03) m/s, next Δt: 20 minutes
[55.56%] i: 800, t: 11.111 days, wall time: 901.974 ms, max(u): (1.123e+00, 1.281e+00, 3.729e-03) m/s, next Δt: 20 minutes
[62.50%] i: 900, t: 12.500 days, wall time: 758.701 ms, max(u): (1.427e+00, 1.295e+00, 4.962e-03) m/s, next Δt: 20 minutes
[69.44%] i: 1000, t: 13.889 days, wall time: 834.873 ms, max(u): (1.430e+00, 1.300e+00, 4.213e-03) m/s, next Δt: 20 minutes
[76.39%] i: 1100, t: 15.278 days, wall time: 817.445 ms, max(u): (1.478e+00, 1.707e+00, 5.020e-03) m/s, next Δt: 20 minutes
[83.33%] i: 1200, t: 16.667 days, wall time: 809.296 ms, max(u): (1.508e+00, 1.510e+00, 4.848e-03) m/s, next Δt: 20 minutes
[90.28%] i: 1300, t: 18.056 days, wall time: 818.400 ms, max(u): (1.607e+00, 1.327e+00, 3.843e-03) m/s, next Δt: 20 minutes
[97.22%] i: 1400, t: 19.444 days, wall time: 732.964 ms, max(u): (1.512e+00, 1.299e+00, 4.576e-03) m/s, next Δt: 20 minutes
[ Info: Simulation is stopping after running for 1.398 minutes.
[ Info: Simulation time 20 days equals or exceeds stop time 20 days.
[ Info: Simulation completed in 1.399 minutes

Visualization

All that's left is to make a pretty movie. Actually, we make two visualizations here. First, we illustrate how to make a 3D visualization with Makie's Axis3 and Makie.surface. Then we make a movie in 2D. We use CairoMakie in this example, but note that using GLMakie is more convenient on a system with OpenGL, as figures will be displayed on the screen.

using CairoMakie

Three-dimensional visualization

We load the saved buoyancy output on the top, north, and east surface as FieldTimeSerieses.

filename = "baroclinic_adjustment"

sides = keys(slicers)

slice_filenames = NamedTuple(side => filename * "_$(side)_slice.jld2" for side in sides)

b_timeserieses = (east   = FieldTimeSeries(slice_filenames.east, "b"),
                  north  = FieldTimeSeries(slice_filenames.north, "b"),
                  top    = FieldTimeSeries(slice_filenames.top, "b"))

B_timeseries = FieldTimeSeries(filename * "_zonal_average.jld2", "b")

times = B_timeseries.times
grid = B_timeseries.grid

48×48×8 RectilinearGrid{Float64, Periodic, Bounded, Bounded} on CPU with 3×3×3 halo
├── Periodic x ∈ [0.0, 1.0e6)          regularly spaced with Δx=20833.3
├── Bounded  y ∈ [-500000.0, 500000.0] regularly spaced with Δy=20833.3
└── Bounded  z ∈ [-1000.0, 0.0]        regularly spaced with Δz=125.0

We build the coordinates. We rescale horizontal coordinates to kilometers.

xb, yb, zb = nodes(b_timeserieses.east)

xb = xb ./ 1e3 # convert m -> km
yb = yb ./ 1e3 # convert m -> km

Nx, Ny, Nz = size(grid)

x_xz = repeat(x, 1, Nz)
y_xz_north = y[end] * ones(Nx, Nz)
z_xz = repeat(reshape(z, 1, Nz), Nx, 1)

x_yz_east = x[end] * ones(Ny, Nz)
y_yz = repeat(y, 1, Nz)
z_yz = repeat(reshape(z, 1, Nz), grid.Ny, 1)

x_xy = x
y_xy = y
z_xy_top = z[end] * ones(grid.Nx, grid.Ny)

Then we create a 3D axis. We use zonal_slice_displacement to control where the plot of the instantaneous zonal average flow is located.

fig = Figure(size = (1600, 800))

zonal_slice_displacement = 1.2

ax = Axis3(fig[2, 1],
           aspect=(1, 1, 1/5),
           xlabel = "x (km)",
           ylabel = "y (km)",
           zlabel = "z (m)",
           xlabeloffset = 100,
           ylabeloffset = 100,
           zlabeloffset = 100,
           limits = ((x[1], zonal_slice_displacement * x[end]), (y[1], y[end]), (z[1], z[end])),
           elevation = 0.45,
           azimuth = 6.8,
           xspinesvisible = false,
           zgridvisible = false,
           protrusions = 40,
           perspectiveness = 0.7)

Axis3()

We use data from the final savepoint for the 3D plot. Note that this plot can easily be animated by using Makie's Observable. To dive into Observables, check out Makie.jl's Documentation.

n = length(times)

41

Now let's make a 3D plot of the buoyancy and in front of it we'll use the zonally-averaged output to plot the instantaneous zonal-average of the buoyancy.

b_slices = (east   = interior(b_timeserieses.east[n], 1, :, :),
            north  = interior(b_timeserieses.north[n], :, 1, :),
            top    = interior(b_timeserieses.top[n], :, :, 1))

# Zonally-averaged buoyancy
B = interior(B_timeseries[n], 1, :, :)

clims = 1.1 .* extrema(b_timeserieses.top[n][:])

kwargs = (colorrange=clims, colormap=:deep, shading=NoShading)

surface!(ax, x_yz_east, y_yz, z_yz;  color = b_slices.east, kwargs...)
surface!(ax, x_xz, y_xz_north, z_xz; color = b_slices.north, kwargs...)
surface!(ax, x_xy, y_xy, z_xy_top;   color = b_slices.top, kwargs...)

sf = surface!(ax, zonal_slice_displacement .* x_yz_east, y_yz, z_yz; color = B, kwargs...)

contour!(ax, y, z, B; transformation = (:yz, zonal_slice_displacement * x[end]),
         levels = 15, linewidth = 2, color = :black)

Colorbar(fig[2, 2], sf, label = "m s⁻²", height = Relative(0.4), tellheight=false)

title = "Buoyancy at t = " * string(round(times[n] / day, digits=1)) * " days"
fig[1, 1:2] = Label(fig, title; fontsize = 24, tellwidth = false, padding = (0, 0, -120, 0))

rowgap!(fig.layout, 1, Relative(-0.2))
colgap!(fig.layout, 1, Relative(-0.1))

save("baroclinic_adjustment_3d.png", fig)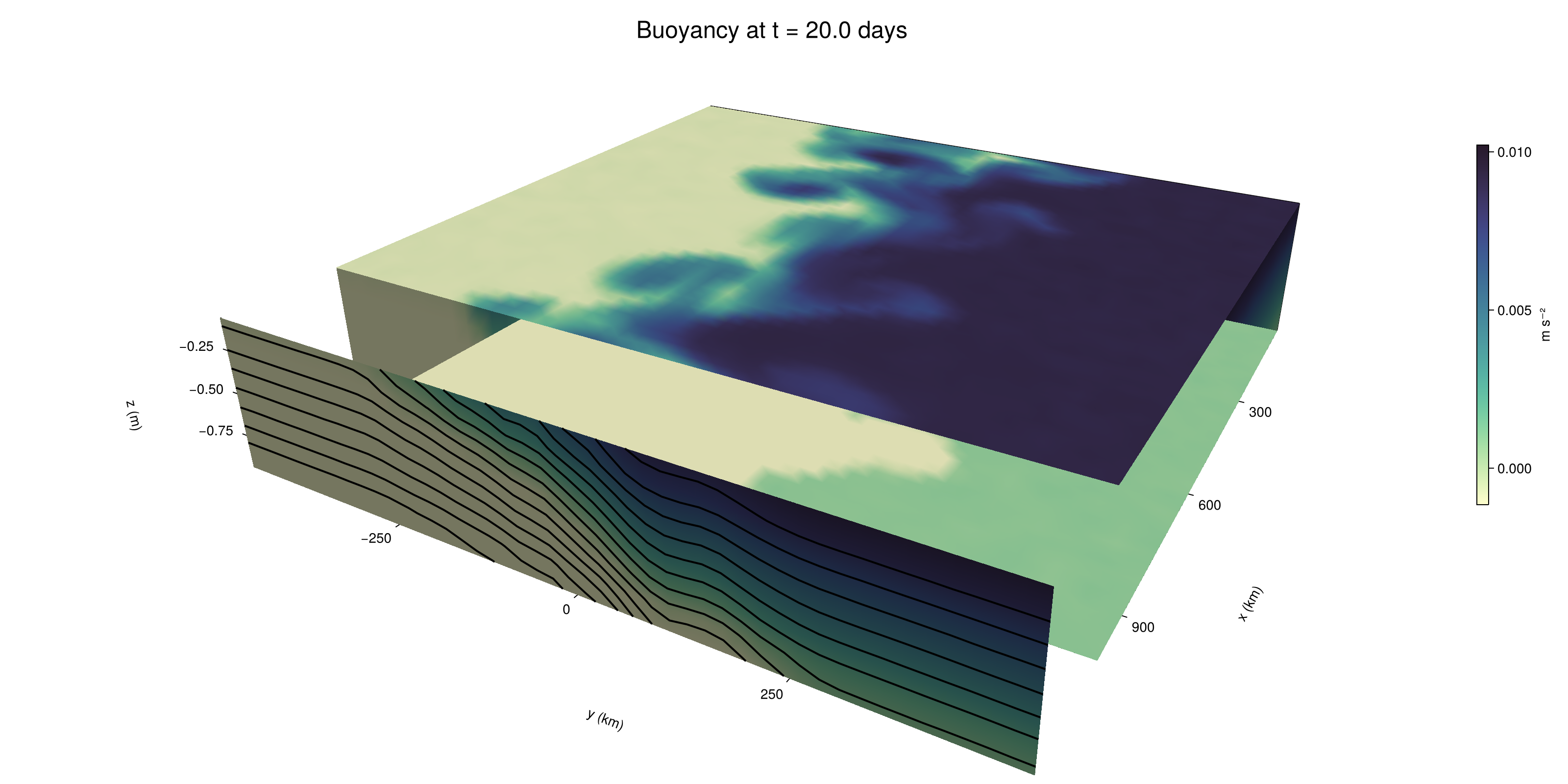

Two-dimensional movie

We make a 2D movie that shows buoyancy $b$ and vertical vorticity $ζ$ at the surface, as well as the zonally-averaged zonal and meridional velocities $U$ and $V$ in the $(y, z)$ plane. First we load the FieldTimeSeries and extract the additional coordinates we'll need for plotting

ζ_timeseries = FieldTimeSeries(slice_filenames.top, "ζ")
U_timeseries = FieldTimeSeries(filename * "_zonal_average.jld2", "u")
B_timeseries = FieldTimeSeries(filename * "_zonal_average.jld2", "b")
V_timeseries = FieldTimeSeries(filename * "_zonal_average.jld2", "v")

xζ, yζ, zζ = nodes(ζ_timeseries)
yv = ynodes(V_timeseries)

xζ = xζ ./ 1e3 # convert m -> km
yζ = yζ ./ 1e3 # convert m -> km
yv = yv ./ 1e3 # convert m -> km

-500.0:20.833333333333332:500.0

Next, we set up a plot with 4 panels. The top panels are large and square, while the bottom panels get a reduced aspect ratio through rowsize!.

fig = Figure(size=(1800, 1000))

axb = Axis(fig[1, 2], xlabel="x (km)", ylabel="y (km)", aspect=1)
axζ = Axis(fig[1, 3], xlabel="x (km)", ylabel="y (km)", aspect=1, yaxisposition=:right)

axu = Axis(fig[2, 2], xlabel="y (km)", ylabel="z (m)")
axv = Axis(fig[2, 3], xlabel="y (km)", ylabel="z (m)", yaxisposition=:right)

rowsize!(fig.layout, 2, Relative(0.3))

To prepare a plot for animation, we index the timeseries with an Observable,

n = Observable(1)

b_top = @lift interior(b_timeserieses.top[$n], :, :, 1)
ζ_top = @lift interior(ζ_timeseries[$n], :, :, 1)
U = @lift interior(U_timeseries[$n], 1, :, :)
V = @lift interior(V_timeseries[$n], 1, :, :)
B = @lift interior(B_timeseries[$n], 1, :, :)

Observable([-0.009394648484885693 -0.008136816322803497 -0.006881122011691332 -0.005643067415803671 -0.004363441374152899 -0.003139625070616603 -0.001871317159384489 -0.0006281745154410601; -0.009378000162541866 -0.008141259662806988 -0.006861047353595495 -0.0056335716508328915 -0.00438250508159399 -0.003116716630756855 -0.0018499168800190091 -0.000623371743131429; -0.009342579171061516 -0.008129914291203022 -0.006845394615083933 -0.005601960700005293 -0.004370208829641342 -0.0031110693234950304 -0.0018587306840345263 -0.0006199748022481799; -0.009365011006593704 -0.008123091422021389 -0.006874402053654194 -0.0056665739975869656 -0.004378949757665396 -0.0031452623661607504 -0.001872752676717937 -0.0006398654659278691; -0.009371929802000523 -0.008106550201773643 -0.006877246778458357 -0.0056116352789103985 -0.0043524811044335365 -0.0031198132783174515 -0.001883004792034626 -0.0006477228016592562; -0.00939199235290289 -0.008146623149514198 -0.006851855665445328 -0.005634952336549759 -0.004365720320492983 -0.003128399606794119 -0.001874452456831932 -0.0006284154369495809; -0.009363886900246143 -0.008127170614898205 -0.006877234671264887 -0.005645427852869034 -0.00436368165537715 -0.0031123505905270576 -0.0018873107619583607 -0.0006223688251338899; -0.00937195960432291 -0.008113156072795391 -0.006888007279485464 -0.005595476366579533 -0.004361634608358145 -0.0031486100051552057 -0.001901865703985095 -0.0006312178447842598; -0.009375461377203465 -0.008089465089142323 -0.006871871184557676 -0.0056107137352228165 -0.00439167907461524 -0.0030959013383835554 -0.0018777584191411734 -0.0006188055267557502; -0.00937611423432827 -0.00813306774944067 -0.006904215551912785 -0.0056212288327515125 -0.004368532449007034 -0.0031204333063215017 -0.0018821791745722294 -0.000628255307674408; -0.00937625952064991 -0.008108782581984997 -0.00688275508582592 -0.005625121761113405 -0.004353545140475035 -0.003099489724263549 -0.0018893879605457187 -0.0006410658243112266; -0.009369317442178726 -0.008112377487123013 -0.00688188849017024 -0.005628013983368874 -0.0043742298148572445 -0.003127890406176448 -0.0018756219651550055 -0.000626673805527389; -0.00939375814050436 -0.008100115694105625 -0.00686725415289402 -0.005612754728645086 -0.004357767291367054 -0.0031308489851653576 -0.0018644917290657759 -0.0006464752950705588; -0.009395831264555454 -0.008087567053735256 -0.006859469693154097 -0.005623254459351301 -0.004375325981527567 -0.0031302154529839754 -0.0018638531910255551 -0.0006460468284785748; -0.009364064782857895 -0.008116573095321655 -0.0068546561524271965 -0.005617039278149605 -0.004366522654891014 -0.0031233581248670816 -0.0018723239190876484 -0.0006308702868409455; -0.00939471647143364 -0.008119945414364338 -0.006880416069179773 -0.005598652176558971 -0.004373833071440458 -0.003106413409113884 -0.0018611899577081203 -0.0006325413123704493; -0.009380662813782692 -0.008134403266012669 -0.006889767944812775 -0.005620728712528944 -0.004396987613290548 -0.0030982207972556353 -0.0018608414102345705 -0.0006362611311487854; -0.009376604110002518 -0.008140805177390575 -0.006898536346852779 -0.00563838891685009 -0.004389541689306498 -0.0031113445293158293 -0.0018696195911616087 -0.0006221826770342886; -0.009385418146848679 -0.00812402181327343 -0.006880662404000759 -0.005617660470306873 -0.004359574988484383 -0.0031185196712613106 -0.0018767535220831633 -0.0006200912757776678; -0.009372314438223839 -0.008131610229611397 -0.006875080522149801 -0.005624729674309492 -0.0043793427757918835 -0.0031146628316491842 -0.0018599925097078085 -0.0006357216625474393; -0.009363384917378426 -0.00813817698508501 -0.0068922871723771095 -0.005613133776932955 -0.004381801467388868 -0.0031153063755482435 -0.001856242073699832 -0.0006269968580454588; -0.00935882143676281 -0.008112872019410133 -0.006881329696625471 -0.005655005108565092 -0.004362576641142368 -0.003124586306512356 -0.0018564206548035145 -0.0006545414798893034; -0.007503335364162922 -0.006282011512666941 -0.005009028594940901 -0.0037409814540296793 -0.0025072437711060047 -0.0012664957903325558 6.151658908493118e-6 0.0012344997376203537; -0.005415563005954027 -0.0041703954339027405 -0.0029042749665677547 -0.0016652727499604225 -0.0004172899352852255 0.0008389270515181124 0.0020799185149371624 0.003363595809787512; -0.00334126316010952 -0.0020992057397961617 -0.0008148532942868769 0.00040942372288554907 0.001665431191213429 0.0029029648285359144 0.004162517376244068 0.005425224080681801; -0.0012318853987380862 -4.056764009874314e-5 0.0012647694675251842 0.0024836091324687004 0.003739219158887863 0.004990943241864443 0.006259532645344734 0.007492334581911564; 0.0006544225616380572 0.0018793119816109538 0.0031266382429748774 0.00436613941565156 0.005615193862468004 0.006909871473908424 0.008114173077046871 0.009381672367453575; 0.0006383152795024216 0.0018779978854581714 0.0031123573426157236 0.004360001999884844 0.0056289867497980595 0.006864638067781925 0.008131559006869793 0.009365822188556194; 0.0006218100897967815 0.0018657735781744123 0.003123846836388111 0.004370774608105421 0.0056207263842225075 0.006869147531688213 0.00815148651599884 0.009389652870595455; 0.0006077735451981425 0.0018837589304894209 0.0031324783340096474 0.004387238062918186 0.0056093186140060425 0.0068813227117061615 0.008127005770802498 0.009357882663607597; 0.0006164066144265234 0.001876253867521882 0.0031372576486319304 0.004366116598248482 0.005609371233731508 0.006867859046906233 0.008089111186563969 0.009388026781380177; 0.0006183359655551612 0.0018897848203778267 0.003103899070993066 0.0043813446536660194 0.005633705295622349 0.0068961214274168015 0.008130907081067562 0.00938291847705841; 0.0006232652231119573 0.001871180604211986 0.003124890150502324 0.004398787394165993 0.00563952699303627 0.006870953366160393 0.008102304302155972 0.009375080466270447; 0.0006167446845211089 0.00185206753667444 0.0031176377087831497 0.004400284960865974 0.005610468331724405 0.006878281943500042 0.008132676593959332 0.009360849857330322; 0.0006274254992604256 0.0018657664768397808 0.0031245690770447254 0.004352355841547251 0.005600735545158386 0.006861627567559481 0.008103342726826668 0.009361130185425282; 0.0006113809067755938 0.0018848894396796823 0.003090178593993187 0.004334837198257446 0.005638916976749897 0.0068586175329983234 0.008106473833322525 0.00938231498003006; 0.0006104400381445885 0.0018917371053248644 0.003154302015900612 0.004352974705398083 0.005637077149003744 0.006855531595647335 0.008105159737169743 0.009380906820297241; 0.000630442111287266 0.0019186672288924456 0.0031210335437208414 0.004396907519549131 0.0056341649033129215 0.006870700512081385 0.008108144626021385 0.009349334053695202; 0.000631284958217293 0.0018852039938792586 0.0031306277960538864 0.004356892313808203 0.005621659569442272 0.006857635919004679 0.008124320767819881 0.009393906220793724; 0.0006625619134865701 0.0018768326845020056 0.003148451680317521 0.004378024954348803 0.005626717582345009 0.006889031734317541 0.008127628825604916 0.009362136013805866; 0.0006115406868048012 0.0018712908495217562 0.0031430195085704327 0.004396823234856129 0.005646246951073408 0.006875760853290558 0.008104504086077213 0.00935108121484518; 0.0006374418153427541 0.0018690312281250954 0.003129011020064354 0.004384550731629133 0.005605226382613182 0.006860119756311178 0.008123302832245827 0.009361098520457745; 0.0006156954332254827 0.0018771585309877992 0.003120073117315769 0.004392052534967661 0.005608363542705774 0.006859235931187868 0.008135871961712837 0.009384339675307274; 0.0005972140934318304 0.0018638353794813156 0.0031366036273539066 0.004381651524454355 0.005630741361528635 0.00689292186871171 0.008135606534779072 0.00937177799642086; 0.0006154626607894897 0.0018801770638674498 0.003120696870610118 0.004361657425761223 0.005624597892165184 0.006875531282275915 0.008108781650662422 0.009385578334331512; 0.0006174920708872378 0.001874985871836543 0.0031610841397196054 0.004373572301119566 0.005620913114398718 0.006885054521262646 0.008123050443828106 0.009383016265928745; 0.000630234950222075 0.001889905077405274 0.003117799060419202 0.004385548643767834 0.005613530986011028 0.00686952518299222 0.008142765611410141 0.009391745552420616; 0.0006238451460376382 0.0018443912267684937 0.0031170665752142668 0.00437020743265748 0.005607193801552057 0.006870148703455925 0.008096721954643726 0.009381258860230446])

and then build our plot:

hm = heatmap!(axb, xb, yb, b_top, colorrange=(0, Δb), colormap=:thermal)
Colorbar(fig[1, 1], hm, flipaxis=false, label="Surface b(x, y) (m s⁻²)")

hm = heatmap!(axζ, xζ, yζ, ζ_top, colorrange=(-5e-5, 5e-5), colormap=:balance)
Colorbar(fig[1, 4], hm, label="Surface ζ(x, y) (s⁻¹)")

hm = heatmap!(axu, yb, zb, U; colorrange=(-5e-1, 5e-1), colormap=:balance)
Colorbar(fig[2, 1], hm, flipaxis=false, label="Zonally-averaged U(y, z) (m s⁻¹)")
contour!(axu, yb, zb, B; levels=15, color=:black)

hm = heatmap!(axv, yv, zb, V; colorrange=(-1e-1, 1e-1), colormap=:balance)
Colorbar(fig[2, 4], hm, label="Zonally-averaged V(y, z) (m s⁻¹)")
contour!(axv, yb, zb, B; levels=15, color=:black)

Finally, we're ready to record the movie.

frames = 1:length(times)

record(fig, filename * ".mp4", frames, framerate=8) do i
    n[] = i
end

This page was generated using Literate.jl.