Minimization of simple loss functions

First we load the required packages.

using Distributions, LinearAlgebra, Random, Plots

using EnsembleKalmanProcesses
using EnsembleKalmanProcesses.ParameterDistributions

const EKP = EnsembleKalmanProcesses

EnsembleKalmanProcesses

Loss function with single minimum

Here, we minimize the loss function

\[G₁(u) = \|u - u_*\| ,\]

where $u$ is a 2-vector of parameters and $u_*$ is given; here $u_* = (-1, 1)$.

u★ = [1, -1]
G₁(u) = [sqrt((u[1] - u★[1])^2 + (u[2] - u★[2])^2)]

We set the seed for pseudo-random number generator for reproducibility.

rng_seed = 41
rng = Random.seed!(Random.GLOBAL_RNG, rng_seed)

We set a stabilization level, which can aid the algorithm convergence

dim_output = 1
stabilization_level = 1e-3
Γ_stabilization = stabilization_level * Matrix(I, dim_output, dim_output)

1×1 Matrix{Float64}:
 0.001

The functional is positive so to minimize it we may set the target to be 0,

G_target = [0]

Prior distributions

As we work with a Bayesian method, we define a prior. This will behave like an "initial guess" for the likely region of parameter space we expect the solution to live in. Here we define $Normal(0,1)$ distributions with no constraints

prior_u1 = constrained_gaussian("u1", 0, 1, -Inf, Inf)
prior_u2 = constrained_gaussian("u1", 0, 1, -Inf, Inf)
prior = combine_distributions([prior_u1, prior_u2])

Calibration

We choose the number of ensemble members and the number of iterations of the algorithm

N_ensemble = 20
N_iterations = 10

The initial ensemble is constructed by sampling the prior

initial_ensemble = EKP.construct_initial_ensemble(rng, prior, N_ensemble)

2×20 Matrix{Float64}:
 -1.50205   0.950787  -2.13389     1.77371  …  0.994771  0.797202  -1.15774
  1.83923  -0.556855   0.0995651  -2.24101     1.25459   0.487004  -1.40943

We then initialize the Ensemble Kalman Process algorithm, with the initial ensemble, the target, the stabilization and the process type (for EKI this is Inversion, initialized with Inversion()).

ensemble_kalman_process = EKP.EnsembleKalmanProcess(initial_ensemble, G_target, Γ_stabilization, Inversion())

Then we calibrate by (i) obtaining the parameters, (ii) calculate the loss function on the parameters (and concatenate), and last (iii) generate a new set of parameters using the model outputs:

for i in 1:N_iterations
    params_i = get_u_final(ensemble_kalman_process)

    g_ens = hcat([G₁(params_i[:, i]) for i in 1:N_ensemble]...)

    EKP.update_ensemble!(ensemble_kalman_process, g_ens)
end

and visualize the results:

u_init = get_u_prior(ensemble_kalman_process)

anim_unique_minimum = @animate for i in 1:N_iterations
    u_i = get_u(ensemble_kalman_process, i)

    plot(
        [u★[1]],
        [u★[2]],
        seriestype = :scatter,
        markershape = :star5,
        markersize = 11,
        markercolor = :red,
        label = "optimum u⋆",
    )

    plot!(
        u_i[1, :],
        u_i[2, :],
        seriestype = :scatter,
        xlims = extrema(u_init[1, :]),
        ylims = extrema(u_init[2, :]),
        xlabel = "u₁",
        ylabel = "u₂",
        markersize = 5,
        markeralpha = 0.6,
        markercolor = :blue,
        label = "particles",
        title = "EKI iteration = " * string(i),
    )
end

The results show that the minimizer of $G_1$ is $u=u_*$.

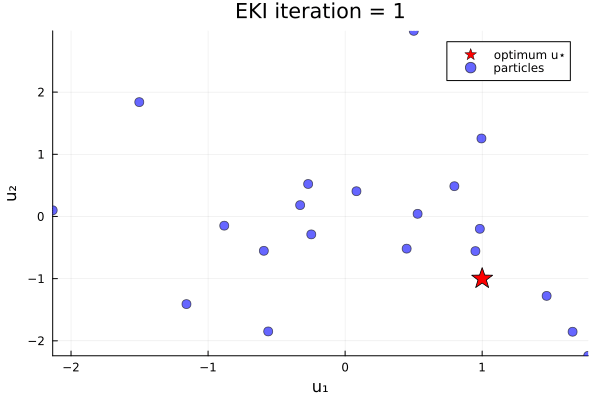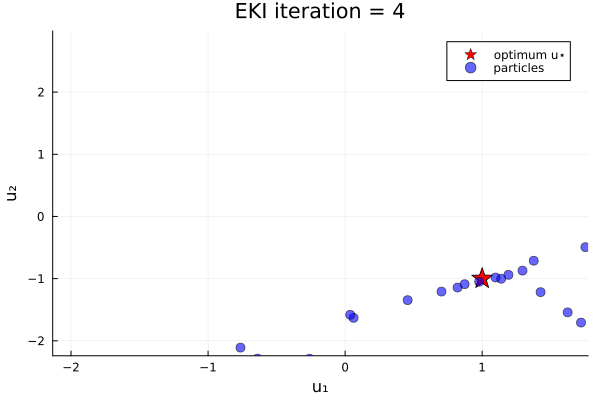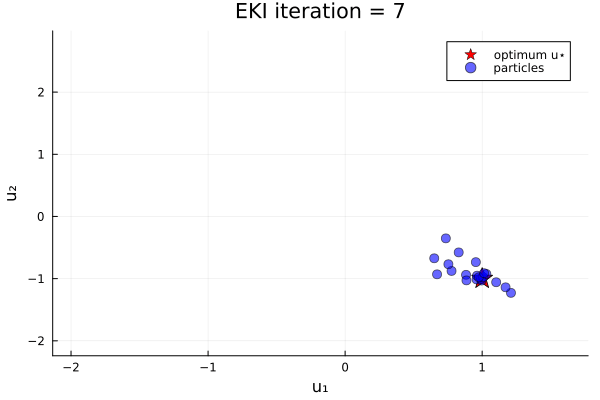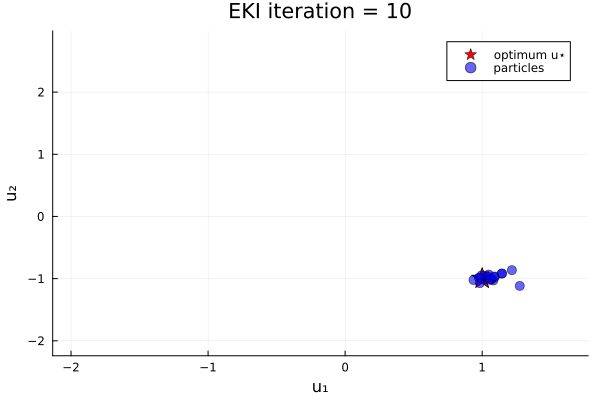
Loss function with two minima

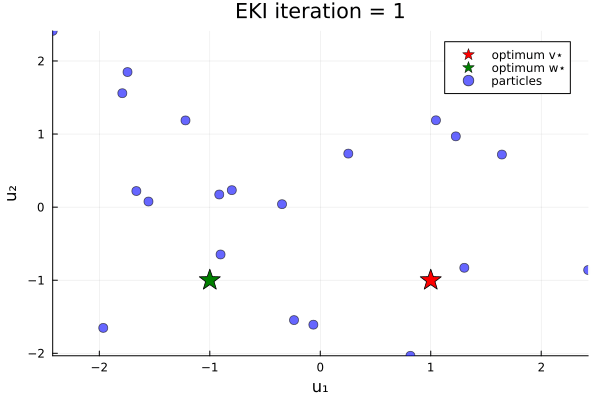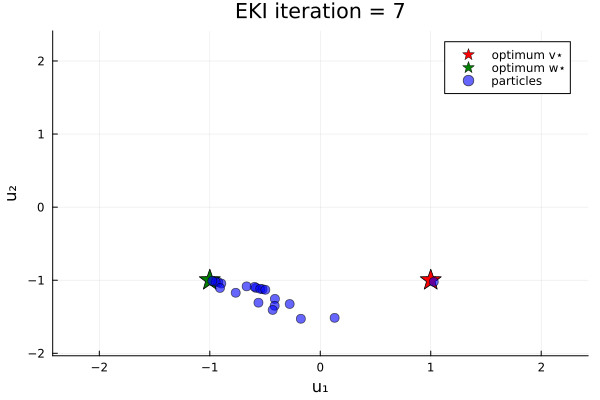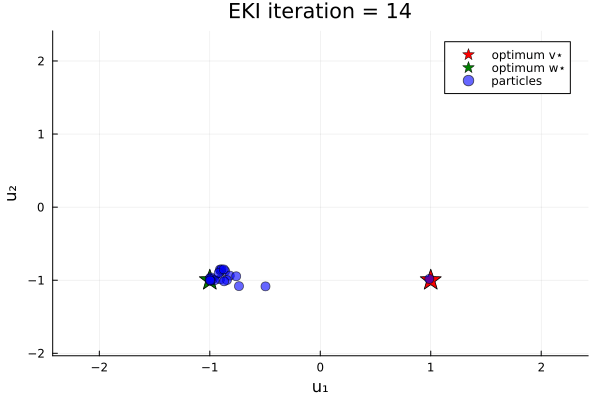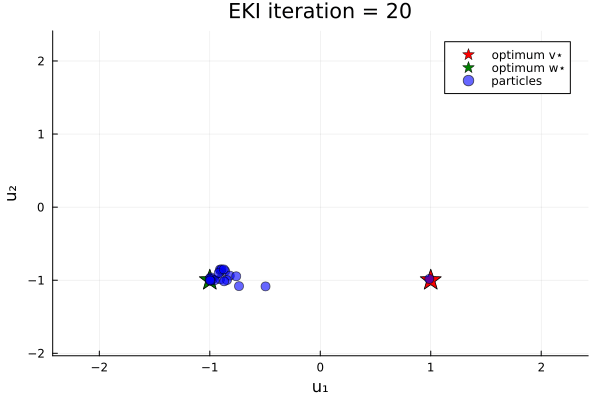
Now let's do an example in which the loss function has two minima. We minimize the loss function

\[G₂(u) = \|u - v_{*}\| \|u - w_{*}\| ,\]

where again $u$ is a 2-vector, and $v_{*}$ and $w_{*}$ are given 2-vectors. Here, we take $v_{*} = (1, -1)$ and $w_{*} = (-1, -1)$.

v★ = [1, -1]
w★ = [-1, -1]
G₂(u) = [sqrt(((u[1] - v★[1])^2 + (u[2] - v★[2])^2) * ((u[1] - w★[1])^2 + (u[2] - w★[2])^2))]

The procedure is same as the single-minimum example above.

We set the seed for pseudo-random number generator for reproducibility,

rng_seed = 10
rng = Random.seed!(Random.GLOBAL_RNG, rng_seed)

A positive function can be minimized with a target of 0,

G_target = [0]

1-element Vector{Int64}:
 0

We choose the stabilization as in the single-minimum example

Prior distributions

We define the prior. We can place prior information on e.g., $u₁$, demonstrating a belief that $u₁$ is more likely to be negative. This can be implemented by setting a bias in the mean of its prior distribution to e.g., $-0.5$:

prior_u1 = constrained_gaussian("u1", -0.5, sqrt(2), -Inf, Inf)
prior_u2 = constrained_gaussian("u1", 0, sqrt(2), -Inf, Inf)
prior = combine_distributions([prior_u1, prior_u2])

ParameterDistribution with 2 entries: 
'u1' with EnsembleKalmanProcesses.ParameterDistributions.Constraint{EnsembleKalmanProcesses.ParameterDistributions.NoConstraint}[Bounds: (-∞, ∞)] over distribution EnsembleKalmanProcesses.ParameterDistributions.Parameterized(Distributions.Normal{Float64}(μ=-0.5, σ=1.4142135623730951)) 
'u1' with EnsembleKalmanProcesses.ParameterDistributions.Constraint{EnsembleKalmanProcesses.ParameterDistributions.NoConstraint}[Bounds: (-∞, ∞)] over distribution EnsembleKalmanProcesses.ParameterDistributions.Parameterized(Distributions.Normal{Float64}(μ=0.0, σ=1.4142135623730951)) 

Calibration

We choose the number of ensemble members, the number of EKI iterations, construct our initial ensemble and the EKI with the Inversion() constructor (exactly as in the single-minimum example):

N_ensemble = 20
N_iterations = 20

initial_ensemble = EKP.construct_initial_ensemble(rng, prior, N_ensemble)

ensemble_kalman_process = EKP.EnsembleKalmanProcess(initial_ensemble, G_target, Γ_stabilization, Inversion())

EnsembleKalmanProcess{Float64, Int64, Inversion, DefaultScheduler{Float64}, DefaultAccelerator}(EnsembleKalmanProcesses.DataContainers.DataContainer{Float64}[EnsembleKalmanProcesses.DataContainers.DataContainer{Float64}([1.3038688926394002 -1.6648606223940248 … -1.7919523047219428 -0.9144972962661588; -0.8300747913927171 0.2203806880175726 … 1.5593414673043817 0.17301324738700036])], [0.0], [0.001;;], 20, EnsembleKalmanProcesses.DataContainers.DataContainer{Float64}[], Float64[], DefaultScheduler{Float64}(1.0), DefaultAccelerator(), Float64[], Inversion(), Random._GLOBAL_RNG(), FailureHandler{Inversion, IgnoreFailures}(EnsembleKalmanProcesses.var"#failsafe_update#28"()), EnsembleKalmanProcesses.Localizers.Localizer{EnsembleKalmanProcesses.Localizers.NoLocalization, Float64}(EnsembleKalmanProcesses.Localizers.var"#1#2"{Matrix{Float64}}([1.0 1.0 1.0; 1.0 1.0 1.0; 1.0 1.0 1.0])), false)

We calibrate by (i) obtaining the parameters, (ii) calculating the loss function on the parameters (and concatenate), and last (iii) generate a new set of parameters using the model outputs:

for i in 1:N_iterations
    params_i = get_u_final(ensemble_kalman_process)

    g_ens = hcat([G₂(params_i[:, i]) for i in 1:N_ensemble]...)

    EKP.update_ensemble!(ensemble_kalman_process, g_ens)
end

and visualize the results:

u_init = get_u_prior(ensemble_kalman_process)

anim_two_minima = @animate for i in 1:N_iterations
    u_i = get_u(ensemble_kalman_process, i)

    plot(
        [v★[1]],
        [v★[2]],
        seriestype = :scatter,
        markershape = :star5,
        markersize = 11,
        markercolor = :red,
        label = "optimum v⋆",
    )

    plot!(
        [w★[1]],
        [w★[2]],
        seriestype = :scatter,
        markershape = :star5,
        markersize = 11,
        markercolor = :green,
        label = "optimum w⋆",
    )

    plot!(
        u_i[1, :],
        u_i[2, :],
        seriestype = :scatter,
        xlims = extrema(u_init[1, :]),
        ylims = extrema(u_init[2, :]),
        xlabel = "u₁",
        ylabel = "u₂",
        markersize = 5,
        markeralpha = 0.6,
        markercolor = :blue,
        label = "particles",
        title = "EKI iteration = " * string(i),
    )
end

Our bias in the prior shifts the initial ensemble into the negative $u_1$ direction, and thus increases the likelihood (over different instances of the random number generator) of finding the minimizer $u=w_*$.

This page was generated using Literate.jl.