GitHub

Minimization of simple loss functions with sparse EKI

How do I run this code?

The full code is found in the examples/ directory of the github repository

First we load the required packages.

using Distributions, LinearAlgebra, Random, Plots

using EnsembleKalmanProcesses
using EnsembleKalmanProcesses.ParameterDistributions
const EKP = EnsembleKalmanProcesses
EnsembleKalmanProcesses

Loss function with single minimum

Here, we minimize the loss function

\[G₁(u) = \|u - u_*\| ,\]

where $u$ is a 2-vector of parameters and $u_*$ is given; here $u_* = (1, 0)$.

u★ = [1, 0]
G₁(u) = [sqrt((u[1] - u★[1])^2 + (u[2] - u★[2])^2)]

We set the seed for pseudo-random number generator for reproducibility.

rng_seed = 41
rng = Random.seed!(Random.GLOBAL_RNG, rng_seed)

We set a stabilization level, which can aid the algorithm convergence

dim_output = 1
stabilization_level = 1e-3
Γ_stabilization = stabilization_level * Matrix(I, dim_output, dim_output)
1×1 Matrix{Float64}:
 0.001

The functional is positive so to minimize it we may set the target to be 0,

G_target = [0]

Prior distributions

As we work with a Bayesian method, we define a prior. This will behave like an "initial guess" for the likely region of parameter space we expect the solution to live in. Here we define $Normal(0,2^2)$ distributions with no constraints

prior_u1 = constrained_gaussian("u1", 0, 2, -Inf, Inf)
prior_u2 = constrained_gaussian("u1", 0, 2, -Inf, Inf)
prior = combine_distributions([prior_u1, prior_u2])
Note

In this example there are no constraints, therefore no parameter transformations.

Calibration

We choose the number of ensemble members and the number of iterations of the algorithm

N_ensemble = 20
N_iterations = 10

The initial ensemble is constructed by sampling the prior

initial_ensemble = EKP.construct_initial_ensemble(rng, prior, N_ensemble)
2×20 Matrix{Float64}:
 -3.0041    1.90157  -4.26778   3.54742  …  1.98954  1.5944    -2.31548
  3.67846  -1.11371   0.19913  -4.48202     2.50918  0.974007  -2.81886

Sparse EKI parameters

γ = 1.0
threshold_value = 1e-2
reg = 1e-3
uc_idx = [1, 2]

process = SparseInversion(γ, threshold_value, uc_idx, reg)
SparseInversion{Float64}(1.0, 0.01, [1, 2], 0.001)

We then initialize the Ensemble Kalman Process algorithm, with the initial ensemble, the target, the stabilization and the process type (for sparse EKI this is SparseInversion).

ensemble_kalman_process = EKP.EnsembleKalmanProcess(initial_ensemble, G_target, Γ_stabilization, process)

Then we calibrate by (i) obtaining the parameters, (ii) calculate the loss function on the parameters (and concatenate), and last (iii) generate a new set of parameters using the model outputs:

for i in 1:N_iterations
    params_i = get_u_final(ensemble_kalman_process)

    g_ens = hcat([G₁(params_i[:, i]) for i in 1:N_ensemble]...)

    EKP.update_ensemble!(ensemble_kalman_process, g_ens)
end
[ Info: [Convex.jl] Compilation finished: 11.57 seconds, 1.050 GiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
┌ Warning: Problem wasn't solved optimally
│   status = ITERATION_LIMIT::TerminationStatusCode = 11
└ @ Convex ~/.julia/packages/Convex/IPPoR/src/solution.jl:124
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
┌ Warning: Problem wasn't solved optimally
│   status = ITERATION_LIMIT::TerminationStatusCode = 11
└ @ Convex ~/.julia/packages/Convex/IPPoR/src/solution.jl:124
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
┌ Warning: Problem wasn't solved optimally
│   status = ITERATION_LIMIT::TerminationStatusCode = 11
└ @ Convex ~/.julia/packages/Convex/IPPoR/src/solution.jl:124
[ Info: [Convex.jl] Compilation finished: 0.01 seconds, 138.031 KiB of memory allocated
┌ Warning: Problem wasn't solved optimally
│   status = ITERATION_LIMIT::TerminationStatusCode = 11
└ @ Convex ~/.julia/packages/Convex/IPPoR/src/solution.jl:124
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
┌ Warning: Problem wasn't solved optimally
│   status = ITERATION_LIMIT::TerminationStatusCode = 11
└ @ Convex ~/.julia/packages/Convex/IPPoR/src/solution.jl:124
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
┌ Warning: Problem wasn't solved optimally
│   status = ITERATION_LIMIT::TerminationStatusCode = 11
└ @ Convex ~/.julia/packages/Convex/IPPoR/src/solution.jl:124
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
┌ Warning: Problem wasn't solved optimally
│   status = ITERATION_LIMIT::TerminationStatusCode = 11
└ @ Convex ~/.julia/packages/Convex/IPPoR/src/solution.jl:124
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
┌ Warning: Problem wasn't solved optimally
│   status = ITERATION_LIMIT::TerminationStatusCode = 11
└ @ Convex ~/.julia/packages/Convex/IPPoR/src/solution.jl:124
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
┌ Warning: Problem wasn't solved optimally
│   status = ITERATION_LIMIT::TerminationStatusCode = 11
└ @ Convex ~/.julia/packages/Convex/IPPoR/src/solution.jl:124
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
┌ Warning: Problem wasn't solved optimally
│   status = ITERATION_LIMIT::TerminationStatusCode = 11
└ @ Convex ~/.julia/packages/Convex/IPPoR/src/solution.jl:124
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
┌ Warning: Problem wasn't solved optimally
│   status = ITERATION_LIMIT::TerminationStatusCode = 11
└ @ Convex ~/.julia/packages/Convex/IPPoR/src/solution.jl:124
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
┌ Warning: Problem wasn't solved optimally
│   status = ITERATION_LIMIT::TerminationStatusCode = 11
└ @ Convex ~/.julia/packages/Convex/IPPoR/src/solution.jl:124
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
┌ Warning: Problem wasn't solved optimally
│   status = ITERATION_LIMIT::TerminationStatusCode = 11
└ @ Convex ~/.julia/packages/Convex/IPPoR/src/solution.jl:124
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
┌ Warning: Problem wasn't solved optimally
│   status = ITERATION_LIMIT::TerminationStatusCode = 11
└ @ Convex ~/.julia/packages/Convex/IPPoR/src/solution.jl:124
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
┌ Warning: Problem wasn't solved optimally
│   status = ITERATION_LIMIT::TerminationStatusCode = 11
└ @ Convex ~/.julia/packages/Convex/IPPoR/src/solution.jl:124
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
┌ Warning: Problem wasn't solved optimally
│   status = ITERATION_LIMIT::TerminationStatusCode = 11
└ @ Convex ~/.julia/packages/Convex/IPPoR/src/solution.jl:124
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
┌ Warning: Problem wasn't solved optimally
│   status = ITERATION_LIMIT::TerminationStatusCode = 11
└ @ Convex ~/.julia/packages/Convex/IPPoR/src/solution.jl:124
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
┌ Warning: Problem wasn't solved optimally
│   status = ITERATION_LIMIT::TerminationStatusCode = 11
└ @ Convex ~/.julia/packages/Convex/IPPoR/src/solution.jl:124
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
┌ Warning: Problem wasn't solved optimally
│   status = ITERATION_LIMIT::TerminationStatusCode = 11
└ @ Convex ~/.julia/packages/Convex/IPPoR/src/solution.jl:124
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
┌ Warning: Problem wasn't solved optimally
│   status = ITERATION_LIMIT::TerminationStatusCode = 11
└ @ Convex ~/.julia/packages/Convex/IPPoR/src/solution.jl:124
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated
[ Info: [Convex.jl] Compilation finished: 0.0 seconds, 138.031 KiB of memory allocated

and visualize the results:

u_init = get_u_prior(ensemble_kalman_process)

anim_unique_minimum = @animate for i in 1:N_iterations
    u_i = get_u(ensemble_kalman_process, i)

    plot(
        [u★[1]],
        [u★[2]],
        seriestype = :scatter,
        markershape = :star5,
        markersize = 11,
        markercolor = :red,
        label = "optimum u⋆",
    )

    plot!(
        u_i[1, :],
        u_i[2, :],
        seriestype = :scatter,
        xlims = extrema(u_init[1, :]),
        ylims = extrema(u_init[2, :]),
        xlabel = "u₁",
        ylabel = "u₂",
        markersize = 5,
        markeralpha = 0.6,
        markercolor = :blue,
        label = "particles",
        title = "EKI iteration = " * string(i),
    )
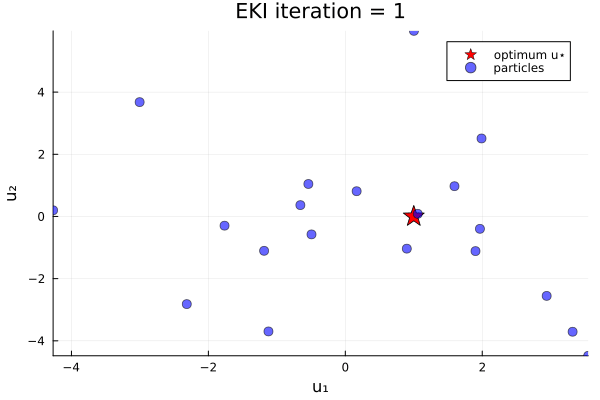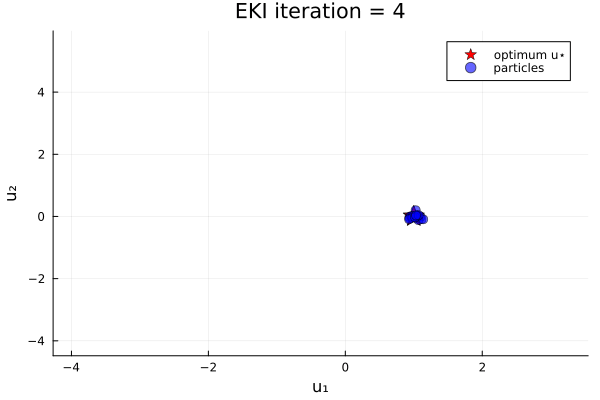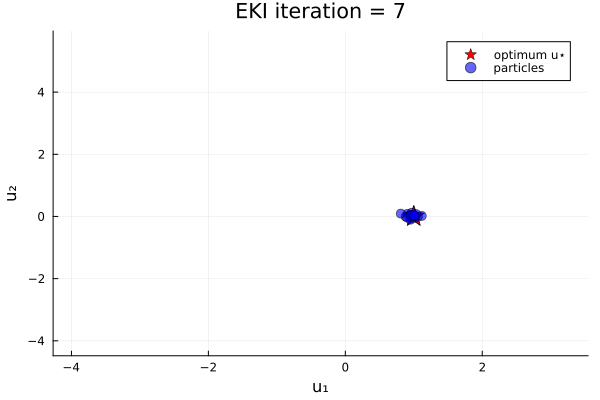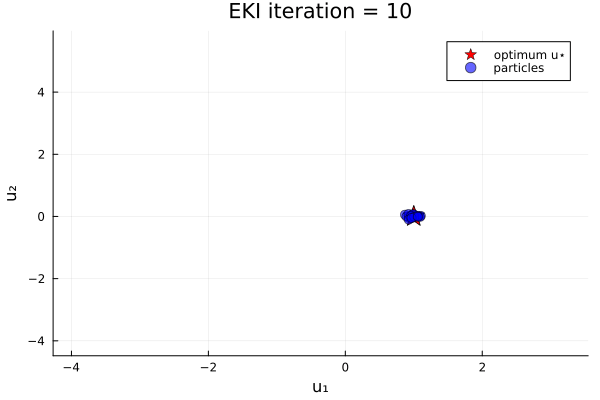
end

The results show that the minimizer of $G_1$ is $u=u_*$.

Example block output

This page was generated using Literate.jl.