GitHub

Implementing Turbulence Closures

This guide shows how to implement a turbulence closure in Oceananigans. We'll build PacanowskiPhilanderVerticalDiffusivity, a Richardson number-based mixing parameterization from Pacanowski and Philander (1981).

The Pacanowski-Philander formulation computes eddy viscosity $\nu$ and diffusivity $\kappa$ as

\[\nu = \nu_0 + \frac{\nu_1}{(1 + c \, Ri)^n}, \quad \kappa = \kappa_0 + \frac{\nu_1}{(1 + c \, Ri)^{n+1}}\]

where $Ri = N^2 / S^2$ is the gradient Richardson number (stratification over shear squared).

Julia's multiple dispatch lets us implement this closure anywhere—a script, a package, or within Oceananigans itself—and it will integrate seamlessly with NonhydrostaticModel and HydrostaticFreeSurfaceModel.

Overview

Turbulence closures add diffusive fluxes to the momentum and tracer equations. The key components are:

  1. Abstract types for dispatch
  2. Diffusivity computation before each time step
  3. Flux functions that use precomputed diffusivities
  4. Time discretization (explicit or vertically implicit)

All closures inherit from AbstractTurbulenceClosure{TimeDiscretization, RequiredHalo}. For scalar diffusivities, we use AbstractScalarDiffusivity{TD, Formulation, RequiredHalo} where Formulation is VerticalFormulation, HorizontalFormulation, or ThreeDimensionalFormulation. See the Turbulence closures documentation for a list of built-in closures.

Step-by-step implementation

Step 1: Define the struct

The closure struct holds its parameters:

using Oceananigans.TurbulenceClosures: AbstractScalarDiffusivity, VerticalFormulation

struct PacanowskiPhilanderVerticalDiffusivity{TD, FT} <: AbstractScalarDiffusivity{TD, VerticalFormulation, 1}
    ν₀ :: FT  # Background viscosity
    ν₁ :: FT  # Shear-driven viscosity coefficient
    κ₀ :: FT  # Background diffusivity
    c  :: FT  # Richardson number scaling coefficient
    n  :: FT  # Exponent for viscosity
    maximum_diffusivity :: FT
    maximum_viscosity :: FT
end

Key points:

  • Type parameters: TD is the time discretization, FT is the float type
  • Supertype: AbstractScalarDiffusivity{TD, VerticalFormulation, 1} indicates:
    • This closure uses scalar (not tensor) diffusivities
    • It only acts in the vertical direction (VerticalFormulation)
    • It requires a halo size of 1
  • All fields are concretely typed: This is essential for type stability and GPU performance

Step 2: Create the constructor

Provide a user-friendly constructor with sensible defaults:

using Oceananigans: VerticallyImplicitTimeDiscretization

function PacanowskiPhilanderVerticalDiffusivity(time_discretization = VerticallyImplicitTimeDiscretization(),
                                                FT = Float64;
                                                ν₀ = 1e-4, ν₁ = 1e-2, κ₀ = 1e-5,
                                                c  = 5.0, n  = 2.0,
                                                maximum_diffusivity = Inf,
                                                maximum_viscosity = Inf)

    TD = typeof(time_discretization)

    return PacanowskiPhilanderVerticalDiffusivity{TD, FT}(
        convert(FT, ν₀),
        convert(FT, ν₁),
        convert(FT, κ₀),
        convert(FT, c),
        convert(FT, n),
        convert(FT, maximum_diffusivity),
        convert(FT, maximum_viscosity))
end

# Test it works
PacanowskiPhilanderVerticalDiffusivity()
Main.PacanowskiPhilanderVerticalDiffusivity{VerticallyImplicitTimeDiscretization, Float64}(0.0001, 0.01, 1.0e-5, 5.0, 2.0, Inf, Inf)

Important conventions:

  • The first positional argument is time_discretization
  • The second positional argument is the float type FT
  • All physics parameters are keyword arguments
  • Always convert to FT to ensure type consistency

Step 3: Define locations and accessors

Diffusivities live at specific grid locations. Vertical diffusivities that multiply vertical gradients belong at (Center, Center, Face). We also define accessors that extract the viscosity and diffusivity from the precomputed fields:

using Oceananigans.Grids: Center, Face
using Oceananigans.TurbulenceClosures

const PPVD = PacanowskiPhilanderVerticalDiffusivity

## Locations
@inline TurbulenceClosures.viscosity_location(::PPVD) = (Center(), Center(), Face())
@inline TurbulenceClosures.diffusivity_location(::PPVD) = (Center(), Center(), Face())

## Accessors (extract from precomputed fields)
@inline TurbulenceClosures.viscosity(::PPVD, diffusivities) = diffusivities.νz
@inline TurbulenceClosures.diffusivity(::PPVD, diffusivities, id) = diffusivities.κz

The id argument is the tracer index, useful for closures with tracer-specific diffusivities.

Step 4: Build closure fields

Closures that precompute diffusivities need storage Fields. Define build_closure_fields to create them:

using Oceananigans.Fields: Field

function TurbulenceClosures.build_closure_fields(grid, clock, tracer_names, bcs, closure::PPVD)
    κz = Field{Center, Center, Face}(grid)
    νz = Field{Center, Center, Face}(grid)
    return (; κz, νz)
end

The returned NamedTuple becomes model.closure_fields and is passed to compute_diffusivities! and flux functions.

Step 5: Implement diffusivity computation

The core of the closure is compute_diffusivities!, which updates diffusivity fields each time step. First, helper functions for the Richardson number:

using Oceananigans.BuoyancyFormulations: ∂z_b
using Oceananigans.Operators: ℑxᶜᵃᵃ, ℑyᵃᶜᵃ, ∂zᶠᶜᶠ, ∂zᶜᶠᶠ

## Square a function evaluation at a point
@inline ϕ²(i, j, k, grid, ϕ, args...) = ϕ(i, j, k, grid, args...)^2

## Compute vertical shear squared at (Center, Center, Face)
@inline function shear_squaredᶜᶜᶠ(i, j, k, grid, velocities)
    ∂z_u² = ℑxᶜᵃᵃ(i, j, k, grid, ϕ², ∂zᶠᶜᶠ, velocities.u)
    ∂z_v² = ℑyᵃᶜᵃ(i, j, k, grid, ϕ², ∂zᶜᶠᶠ, velocities.v)
    return ∂z_u² + ∂z_v²
end

## Compute Richardson number at (Center, Center, Face)
@inline function Riᶜᶜᶠ(i, j, k, grid, velocities, buoyancy, tracers)
    S² = shear_squaredᶜᶜᶠ(i, j, k, grid, velocities)
    N² = ∂z_b(i, j, k, grid, buoyancy, tracers)
    S²_min = eps(eltype(grid))
    Ri = max(zero(grid), N²) / max(S², S²_min)
    return Ri
end

Now the main function and GPU kernel:

using Oceananigans.Utils: launch!
using Oceananigans.TurbulenceClosures: buoyancy_tracers, buoyancy_force
using KernelAbstractions: @kernel, @index

function TurbulenceClosures.compute_diffusivities!(diffusivities, closure::PPVD, model; parameters = :xyz)
    arch = model.architecture
    grid = model.grid
    tracers = buoyancy_tracers(model)
    buoyancy = buoyancy_force(model)
    velocities = model.velocities

    launch!(arch, grid, parameters,
            compute_pp_diffusivities!, diffusivities, grid, closure, velocities, tracers, buoyancy)

    return nothing
end

@kernel function compute_pp_diffusivities!(diffusivities, grid, closure, velocities, tracers, buoyancy)
    i, j, k = @index(Global, NTuple)

    Ri = Riᶜᶜᶠ(i, j, k, grid, velocities, buoyancy, tracers)

    ## Extract parameters
    ν₀ = closure.ν₀
    ν₁ = closure.ν₁
    κ₀ = closure.κ₀
    c  = closure.c
    n  = closure.n

    ## Pacanowski-Philander formulas
    denominator = 1 + c * Ri
    νz = ν₀ + ν₁ / denominator^n
    κz = κ₀ + ν₁ / denominator^(n + 1)

    ## Apply maximum limits
    νz = min(νz, closure.maximum_viscosity)
    κz = min(κz, closure.maximum_diffusivity)

    @inbounds diffusivities.νz[i, j, k] = νz
    @inbounds diffusivities.κz[i, j, k] = κz
end

GPU compatibility rules for kernels:

  • Use @kernel from KernelAbstractions.jl
  • Use @index(Global, NTuple) to get indices
  • Use @inbounds for array access
  • Never use if/else with different types—use ifelse instead
  • Never throw errors—GPU kernels cannot print or throw
  • Avoid allocations

Step 6: Implement show methods

Good display methods help users understand their closures:

using Oceananigans.Utils: prettysummary

Base.summary(closure::PPVD{TD}) where TD =
    string("PacanowskiPhilanderVerticalDiffusivity{$TD}")

function Base.show(io::IO, closure::PPVD)
    print(io, summary(closure), ":\n")
    print(io, "├── ν₀: ", prettysummary(closure.ν₀), '\n')
    print(io, "├── ν₁: ", prettysummary(closure.ν₁), '\n')
    print(io, "├── κ₀: ", prettysummary(closure.κ₀), '\n')
    print(io, "├── c: ", prettysummary(closure.c), '\n')
    print(io, "└── n: ", prettysummary(closure.n))
end

# Test it
PacanowskiPhilanderVerticalDiffusivity()
PacanowskiPhilanderVerticalDiffusivity{VerticallyImplicitTimeDiscretization}:
├── ν₀: 0.0001
├── ν₁: 0.01
├── κ₀: 1.0e-5
├── c: 5.0
└── n: 2.0

Simulating a wind-driven boundary layer

Let's test the closure by comparing it with CATKEVerticalDiffusivity and TKEDissipationVerticalDiffusivity in a wind-driven boundary layer simulation.

First, we set up the simulation parameters:

using Oceananigans
using Oceananigans.Units

Lz = 256       # Domain depth (m)
Nz = 64        # Vertical resolution
N² = 1e-5      # Background stratification (s⁻²)
τˣ = -1e-4     # Surface kinematic stress (m² s⁻²), i.e. wind stress / density
Jᵇ = 0         # Surface buoyancy flux (m² s⁻³)
f  = 1e-4      # Coriolis parameter (s⁻¹)

stop_time = 2days

We'll create a helper function to set up and run simulations:

function run_boundary_layer(closure; stop_time)
    grid = RectilinearGrid(size=Nz, z=(-Lz, 0), topology=(Flat, Flat, Bounded))

    u_bcs = FieldBoundaryConditions(top = FluxBoundaryCondition(τˣ))
    b_bcs = FieldBoundaryConditions(top = FluxBoundaryCondition(Jᵇ))

    model = HydrostaticFreeSurfaceModel(grid;
                                        closure,
                                        buoyancy = BuoyancyTracer(),
                                        tracers = :b,
                                        coriolis = FPlane(f=f),
                                        boundary_conditions = (u=u_bcs, b=b_bcs))

    set!(model, b = z -> N² * z)  # linear stratification

    simulation = Simulation(model; Δt=10minutes, stop_time)
    conjure_time_step_wizard!(simulation, cfl=0.5, max_Δt=10minutes)
    run!(simulation)

    return model
end

Run all three closures:

## Run with Pacanowski-Philander
pp_closure = PacanowskiPhilanderVerticalDiffusivity(ν₁=5e-3, c=5.0)
model_pp = run_boundary_layer(pp_closure; stop_time)

## Run with CATKE
catke_closure = CATKEVerticalDiffusivity()
model_catke = run_boundary_layer(catke_closure; stop_time)

## Run with TKE-Dissipation (k-ε style)
tked_closure = TKEDissipationVerticalDiffusivity()
model_tked = run_boundary_layer(tked_closure; stop_time)
[ Info: Initializing simulation...
[ Info:     ... simulation initialization complete (433.725 ms)
[ Info: Executing initial time step...
[ Info:     ... initial time step complete (2.500 seconds).
[ Info: Simulation is stopping after running for 3.177 seconds.
[ Info: Simulation time 2 days equals or exceeds stop time 2 days.
[ Info: Initializing simulation...
[ Info:     ... simulation initialization complete (90.112 ms)
[ Info: Executing initial time step...
[ Info:     ... initial time step complete (2.065 seconds).
[ Info: Simulation is stopping after running for 3.470 seconds.
[ Info: Simulation time 2 days equals or exceeds stop time 2 days.
[ Info: Initializing simulation...
[ Info:     ... simulation initialization complete (85.909 ms)
[ Info: Executing initial time step...
[ Info:     ... initial time step complete (2.688 seconds).
[ Info: Simulation is stopping after running for 4.246 seconds.
[ Info: Simulation time 2 days equals or exceeds stop time 2 days.

Let's visualize the resulting boundary layer profiles:

using CairoMakie

fig = Figure(size=(1000, 400))

z_pp = znodes(model_pp.tracers.b)
z_catke = znodes(model_catke.tracers.b)
z_tked = znodes(model_tked.tracers.b)

## Buoyancy profiles
ax1 = Axis(fig[1, 1], xlabel="Buoyancy (m s⁻²)", ylabel="z (m)",
           title="Buoyancy profile")

lpp = lines!(ax1, interior(model_pp.tracers.b, 1, 1, :), z_pp,
             label="Pacanowski-Philander", linewidth=2)
lcatke = lines!(ax1, interior(model_catke.tracers.b, 1, 1, :), z_catke,
                label="CATKE", linewidth=2, linestyle=:dash)
ltked = lines!(ax1, interior(model_tked.tracers.b, 1, 1, :), z_tked,
               label="TKE-Dissipation", linewidth=2, linestyle=:dot)

## Velocity profiles
ax2 = Axis(fig[1, 2], xlabel="Velocity (m s⁻¹)", ylabel="z (m)",
           title="Zonal velocity")

lines!(ax2, interior(model_pp.velocities.u, 1, 1, :), z_pp,
       label="PP", linewidth=2)
lines!(ax2, interior(model_catke.velocities.u, 1, 1, :), z_catke,
       label="CATKE", linewidth=2, linestyle=:dash)
lines!(ax2, interior(model_tked.velocities.u, 1, 1, :), z_tked,
       label="TKE-ϵ", linewidth=2, linestyle=:dot)

## Diffusivity profiles
ax3 = Axis(fig[1, 3], xlabel="Diffusivity (m² s⁻¹)", ylabel="z (m)",
           title="Tracer diffusivity", xscale=log10)

z_face_pp = znodes(model_pp.closure_fields.κz)
κ_pp = interior(model_pp.closure_fields.κz, 1, 1, :)
κ_pp_plot = max.(κ_pp, 1e-6)  ## Avoid log of zero
lines!(ax3, κ_pp_plot, z_face_pp, label="PP", linewidth=2)

z_face_catke = znodes(model_catke.closure_fields.κc)
κ_catke = interior(model_catke.closure_fields.κc, 1, 1, :)
κ_catke_plot = max.(κ_catke, 1e-6)
lines!(ax3, κ_catke_plot, z_face_catke, label="CATKE", linewidth=2, linestyle=:dash)

z_face_tked = znodes(model_tked.closure_fields.κu)
κ_tked = interior(model_tked.closure_fields.κu, 1, 1, :)
κ_tked_plot = max.(κ_tked, 1e-6)
lines!(ax3, κ_tked_plot, z_face_tked, label="TKE-ε", linewidth=2, linestyle=:dot)

fig[2, :] = Legend(fig, [lpp, lcatke, ltked], ["Pacanowski-Philander", "CATKE", "TKE-ε"],
                   orientation = :horizontal, tellwidth = false, framevisible = false)

rowsize!(fig.layout, 2, Auto(0.15))  # adjust legend row height
rowgap!(fig.layout, 10)

fig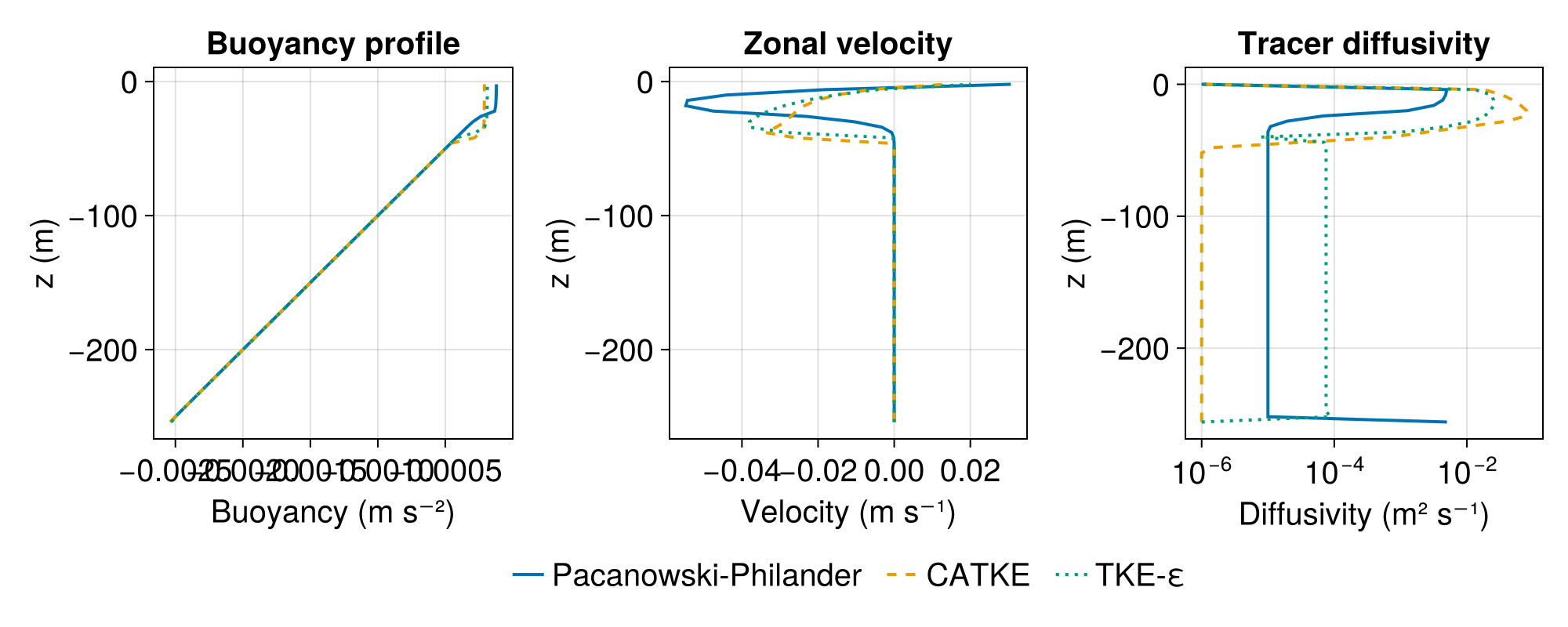
Example block output

The comparison reveals differences in how the closures parameterize mixing:

  • Pacanowski-Philander uses a local Richardson number formulation, producing smooth diffusivity profiles that respond directly to the local shear and stratification
  • CATKEVerticalDiffusivity uses a prognostic TKE equation that captures non-local effects and produces sharper transitions at the boundary layer base
  • TKEDissipationVerticalDiffusivity (k-ε) uses two prognostic equations (for TKE and dissipation rate) allowing independent control of mixing length scales

How diffusivities become fluxes

  1. compute_diffusivities! is called during update_state!
  2. Precomputed diffusivities are stored in model.closure_fields
  3. During tendency computation, flux functions (diffusive_flux_z, viscous_flux_uz, etc.) use the viscosity() and diffusivity() accessors

For AbstractScalarDiffusivity, flux functions are already implemented—you don't need to write them.

Time discretization

Two options for diffusive terms:

ExplicitTimeDiscretization — simple but has a diffusive CFL constraint:

using Oceananigans.TurbulenceClosures: ExplicitTimeDiscretization

closure = PacanowskiPhilanderVerticalDiffusivity(ExplicitTimeDiscretization())
PacanowskiPhilanderVerticalDiffusivity{ExplicitTimeDiscretization}:
├── ν₀: 0.0001
├── ν₁: 0.01
├── κ₀: 1.0e-5
├── c: 5.0
└── n: 2.0

VerticallyImplicitTimeDiscretization (default) — stable for large diffusivities, uses a tridiagonal solver:

closure = PacanowskiPhilanderVerticalDiffusivity(VerticallyImplicitTimeDiscretization())
PacanowskiPhilanderVerticalDiffusivity{VerticallyImplicitTimeDiscretization}:
├── ν₀: 0.0001
├── ν₁: 0.01
├── κ₀: 1.0e-5
├── c: 5.0
└── n: 2.0

Advanced features

Closures that require extra tracers

Some closures (like CATKEVerticalDiffusivity) require prognostic equations for additional quantities (like TKE). Implement:

closure_required_tracers(::MyClosure) = (:e,)  # requires tracer named :e

Closures that modify boundary conditions

Some closures need special boundary conditions. Implement:

add_closure_specific_boundary_conditions(closure::MyClosure, bcs, args...) = modified_bcs

Custom flux functions

For non-standard flux formulations (like tensor diffusivities for isopycnal mixing), you can override the flux functions directly. See IsopycnalSkewSymmetricDiffusivity for an example.

Testing

Create tests that verify:

  1. Construction: The closure constructs with default and custom parameters
  2. Type stability: Use @code_warntype on critical functions
  3. GPU compatibility: Run on GPU to catch dynamic dispatch issues
  4. Physical behavior: Test that diffusivities respond correctly to flow conditions
  5. Conservation: Verify that the closure doesn't create or destroy tracer mass

Example test:

using Test

closure = PacanowskiPhilanderVerticalDiffusivity()
grid = RectilinearGrid(size=(4, 4, 4), extent=(1, 1, 1))
model = NonhydrostaticModel(grid; closure=closure, buoyancy=BuoyancyTracer(), tracers=:b)

@test model isa NonhydrostaticModel

time_step!(model, 1)
@test model.clock.time == 1
Test Passed

Contributing your closure to Oceananigans

The closure we implemented above works immediately—you can use it in any script or package. Julia's multiple dispatch means the methods we defined integrate seamlessly with Oceananigans without modifying the source code.

If you'd like to contribute your closure to Oceananigans itself, here are the additional steps:

1. Create a source file

Place your implementation in a file under src/TurbulenceClosures/turbulence_closure_implementations/. For example:

src/TurbulenceClosures/turbulence_closure_implementations/pacanowski_philander_vertical_diffusivity.jl

2. Include the file

Add an include statement in src/TurbulenceClosures/TurbulenceClosures.jl:

include("turbulence_closure_implementations/pacanowski_philander_vertical_diffusivity.jl")

3. Export the closure

Add the closure to the exports in TurbulenceClosures.jl:

export PacanowskiPhilanderVerticalDiffusivity

And if it should be part of the top-level public API, also export it from src/Oceananigans.jl.

4. Add documentation

  • Add a docstring to the constructor
  • Add an entry to the Turbulence closures documentation page
  • Add any references to docs/oceananigans.bib

5. Write tests

Add tests to the test suite in test/ following existing patterns.

6. Open a pull request

Follow the Contributors Guide to submit your implementation for review.

Summary

To implement a turbulence closure:

  1. Define a struct inheriting from an appropriate abstract type
  2. Create a constructor with sensible defaults
  3. Specify locations and accessors for viscosity/diffusivity
  4. Build fields with build_closure_fields
  5. Compute diffusivities with compute_diffusivities!
  6. Add display methods with summary and show

That's it! Your closure is ready to use. Contributing to Oceananigans is optional but helps the community benefit from your work.